Este circuito de corrente alternada em série, com frequência angular , descrito pelo gráfico de fasores abaixo.
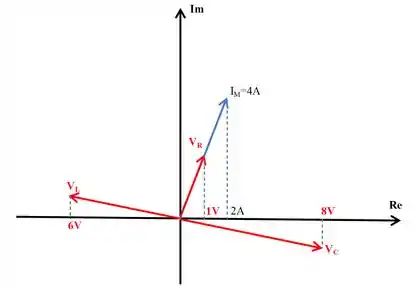
Determine a frequência de ressonância do circuito.
Qual é a diferença de fase entre a corrente e a voltagem na fonte?
Determine a impedância do circuito.
Esboce o gráfico de fasores de todas as voltagens e da corrente para quando o sistema entra em ressonância.
Passo 1
Para resolver essa questão, vamos começar determinando os valores de , , . Como , o ângulo entre o vetor e o eixo horizontal é . Portanto, esse é o mesmo ângulo entre e o eixo horizontal:
Analogamente, o ângulo entre e o eixo horizontal é :
E o ângulo entre e o eixo horizontal é :
Agora que temos os valores das tensões e da amplitude da corrente, podemos determinar as impedâncias e , sabendo o valor de , podemos determinar o valor da indutância e da capacitância.
Para a indutância, temos:
Analogamente para a capacitância:
Agora que sabemos e , podemos determinar a frequência angular de ressonância:
Passo 2
Para determinar a constante de fase entre a tensão e a corrente, vamos primeiro terminar as componentes da tensão:
Logo, a resultante da tensão é:
Para determinar o ângulo entre e , podemos usar a seguinte relação:
Passo 3
Para determinar a impedância, podemos usar a seguinte relação:
substituindo os valores, temos:
Passo 4
Quando o circuito entra em ressonância, temos que , logo, a tensão , que é a soma vetorial das tensões dos dispositivos no circuito, é igual à , e portanto, está em fase com a corrente. O diagrama fasorial, quando o circuito entra em ressonância é:
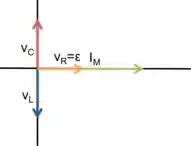
Resposta