Uma bobina formada por um conjunto de espiras de lados e está imersa em um campo magnético de . Ela pode ser girada através de uma manivela que se encontra fixa às suas extremidades. Esta manivela possui um mecanismo que só permite que ela gire em uma direção tal que a parte superior da bobina sempre está entrando na página, como mostra a figura.
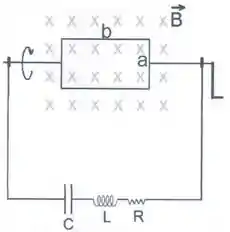
5) Sabendo que a bobina parte do repouso com seu plano perpendicular à página, como mostra a figura, ache a expressão para a força eletromotriz em função do tempo sabendo que a frequência angular da bobina é de .
(a)
(b)
(c)
(d)
(e)
Esta bobina é ligada então a um circuito em série, onde , e , como mostra a figura.
6) O circuito da figura tem características:
(a) resistivas, pois a voltagem do circuito está em fase com a corrente.
(b) indutivas, pois a voltagem do circuito está adiantada em relação à corrente.
(c) indutivas, pois a voltagem do circuito está atrasada em relação à corrente.
(d) capacitivas, pois a voltagem do circuito está adiantada em relação à corrente.
(e) capacitivas, pois a voltagem do circuito está atrasada em relação à corrente.
Passo 1
Vamos, inicialmente, calcular o fluxo magnético para uma espira:
onde .
Passo 2
Sabemos que a fem induzida é dada por:
onde é o número total de espiras.
Temos:
Passo 3
Vamos calcular as reatâncias capacitiva e indutiva, e :
Como , o circuito tem características capacitivas. Nesse caso, é negativo e o fasor está adiantado em relação ao fasor .
Resposta
5) (b)
6) (e) capacitivas, pois a voltagem do circuito está atrasada em relação à corrente.