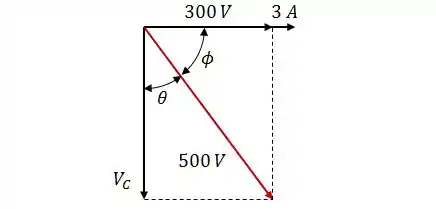
O circuito da figura é usado para determinar a capacitância do capacitor.
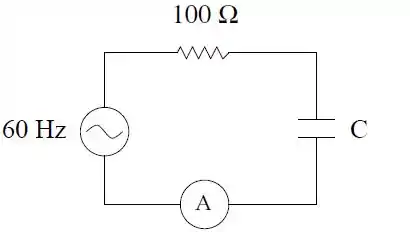
O resistor tem resistência de e a fonte de tensão é um gerador de com frequência de e tensão eficaz de . A leitura do amperímetro que mede o valor eficaz da corrente é .
Faça um diagrama indicando claramente os fasores da corrente e das tensões no gerador, resistor e capacitor. Determine a capacitância do capacitor.
Calcule a potência média consumida pelo circuito e o fator de potência.
Admitindo-se que para tem-se um pico de tensão no gerador, determine a tensão instantânea no capacitor.
Passo 1
Faça um diagrama indicando claramente os fasores da corrente e das tensões no gerador, resistor e capacitor. Determine a capacitância do capacitor.
A relação entre a tensão eficaz e as tensões no resistor e no capacitor é dada por:
Onde:
Assim, a tensão no capacitor será dada por:
Sabendo que a tensão no capacitor é atrasada em , o diagrama de fasores terá essa cara:
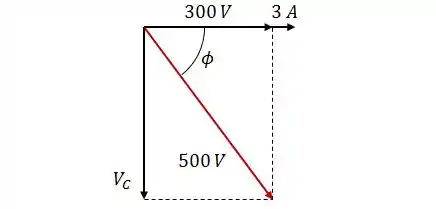
Passo 2
Agora que já calculamos a tensão no capacitor, ficou tranquilo pra calcularmos a capacitância:
Onde é a reatância capacitiva, dada por:
Passo 3
Calcule a potência média consumida pelo circuito e o fator de potência.
O único elemento do circuito que dissipa potência é o resistor, logo, calcular a potência média dissipada é a mesma coisa que calcular a potência dissipada no resistor, entendeu?
Então vamos nessa.
Passo 4
O fator de potência é dado por:
Dando uma olhada no diagrama de fasores, vemos que o fator de potência será:
Passo 5
Admitindo-se que para tem-se um pico de tensão no gerador, determine a tensão instantânea no capacitor.
O que nós temos que calcular aqui é a tensão no capacitor em função do tempo.
Quando o problema diz que, em tem-se um pico de tensão no gerador, é porque podemos escrever a tensão no gerador como:
Sabendo que a tensão no capacitor está atrasada em relação à tensão da fonte, tensão vai ter essa cara:
Onde:
Além disso, como é a tensão eficaz no capacitor, a tensão máxima no capacitor é dada por:
Portanto:
Resposta