Sobre uma bobina formada por um conjunto de espiras de área é aplicado um campo magnético uniforme perpendicular à sua área, onde este varia no tempo do forma . Esta bobina é ligada, então, a um circuito RLC dado na figura.
A corrente máxima do circuito vale:
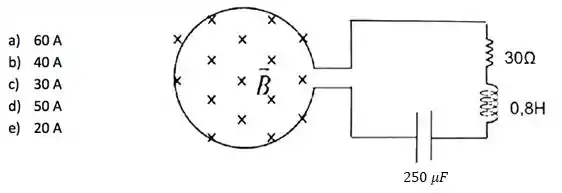
Passo 1
Neste caso, temos um fluxo magnético variável com o tempo devido ao campo magnético uniforme e variável com o tempo (ou não estacionário!). Bom, antes de qualquer, o que significa um campo ser uniforme e variável no tempo?
Significa que em cada instante de tempo , o campo magnético sobre todos os pontos da área definida pelas espiras da bobina tem o mesmo valor. Ou seja, se estamos no instante de tempo , todos os pontos da área terão o mesmo valor . Em um instante posterior , o campo em todos os pontos da área terão o mesmo valor . Isso é importante manter em mente, pessoal, porque várias questões, se não a maioria delas, falam de um campo magnético uniforme e estacionário, cujas características são fundamentais.
Passo 2
Na caso propriamente desta questão, para um instante de tempo arbitrário, como o campo tem o mesmo valor sobre todos os pontos da área da bobina e podemos considerá-lo como paralelo à área da bobina, podemos escrever que o fluxo magnético é
pois é paralelo ao vetor e também tem o mesmo valor sobre todos os pontos da superfície .
Como o campo magnético oscila no tempo, teremos o módulo da fem induzida com a seguinte forma
Portanto, o valor máximo da fem induzida é . A corrente máxima é
em que é a impedância do circuito RLC considerado, que encontraremos no próximo passo.
Passo 3
Em um circuito RLC, a impedância é dada por
em que é a reatância indutiva e é a reatância capacitiva. Substituindo os valores dados no enunciado, encontramos que
o que nos dá uma impedância de
Portanto, a corrente máxima no circuito é
Resposta
A reposta correta é a letra d).