A altura de um corpo que se desloca verticalmente é dada por:
Com em metros e em segundos. Determine a altura máxima do corpo.
Passo 1
Deve-se desenhar o problema e anotar as condições dadas, o que é super importante para um melhor entendimento do problema.
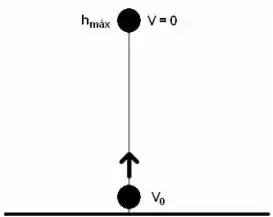
Passo 2
Analisando a equação e o esquema, chegamos na função que desejamos otimizar em função de apenas uma variável.
Note, que (velocidade inicial), (aceleração da gravidade) e (posição inicial) são valores constantes. Deste modo, o tempo é a única variável.
Para encontrar o máximo da função , vamos derivar essa função.
Passo 3
Agora, para achar o ponto de máximo, temos que encontrar os pontos críticos. Para isso, derivamos:
Os pontos críticos ocorrem onde a derivada não existe ou é zero. Como se trata de um polinômio, ela vai sempre existir. Vamos ver quando será zero:
Passo 4
Analisamos os sinais das derivadas antes e depois dos pontos críticos para garantir que sejam máximo ou mínimo.
Uma forma de determinar a presença de máximos e mínimos e pelo teste da segunda derivada. Então vamos aplicá-lo:
Como a questão garante que . A segunda derivada é negativa no ponto crítico, ou seja, temos um ponto de máximo.
Passo 5
Caso achemos mais de um ponto crítico, temos que testá-los na função para ver qual deles é melhor (que dá um valor de máximo maior ou um valor de mínimo menor).
Não há outros pontos críticos na função, então não precisamos comparar com outros pontos.
Passo 6
Vamos verificar agora as fronteiras (menor e maior tempos) para garantir que este é um máximo global (altura máxima).
A função começa em (menor tempo), uma vez que o tempo não pode ser negativo. Para tal valor:
Para o maior tempo, vamos considerar , então vamos aplicar o limite:
No Passo 3, encontramos o ponto crítico:
Comparando os valores de menor e maior tempo com o ponto crítico, vemos que é máximo global.
Assim, o para esse tempo será: