Um cilindro homogêneo, de raio e massa , rola sem deslizar sobre um plano horizontal,
deslocando-se com velocidade , até alcançar um plano com inclinação , continuando a rolar sem deslizamento, descendo ao longo de um comprimento até atingir um novo plano horizontal.
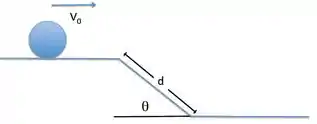
a) Qual o trabalho realizado no processo pela força peso?
b) Qual a velocidade do cilindro na base do plano inclinado?
c) Qual o coeficiente de atrito mínimo para que o cilindro desça o plano inclinado sem deslizar?
Dê suas respostas em termos de , ,,, . Dado: momento de inércia do cilindro .
Passo 1
a)
O trabalho da força peso será dado por:
Sendo o a diferença de altura do plano inclinado, que nada mais nada menos é que . Assim, teremos:
Passo 2
b)
Pelo Teorema Trabalho-Variação da Energia Cinética, teremos:
Mas sabemos que a energia cinética pode ser dividia em energia cinética de rotação e de translação, logo:
Como,
Ah, só mais uma coisa, lá do movimento circular a gente sabe que:
Logo:
Passo 3
Para saber o coeficiente de atrito mínimo para manter o rolamento sem deslizamento, temos que achar o coeficiente de atrito estático máximo, ou seja, que o bloco não escorregue, só role. Assim a força de atrito pode ser calculada por .
Isolando as forças e decompondo a força peso como na figura, teremos:
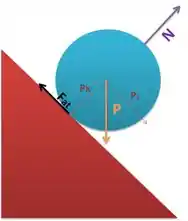
Pela 2ª Lei de Newton, teremos:
Passo 4
Usando as Leis de Newton para rotação, teremos:
E substituindo a relação que achamos para a aceleração, vamos ter:
Logo: