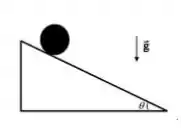
Uma esfera homogênea de massa e raio , inicialmente em repouso, rola sem deslizar sobre um plano inclinado que forma um ângulo com a horizontal (ver figura). O momento de inércia da esfera ao redor do seu centro de massa é . A aceleração gravitacional é .
(a) Desenhe todas as forças atuando na esfera, indicando o seu ponto de aplicação.
(b) Calcule a força de atrito entre a esfera e o plano inclinado.
(c) Suponha, agora, que a esfera esteja rolando na iminência de deslizar. Determine o coeficiente de atrito estático entre a esfera e o plano inclinado.
Passo 1
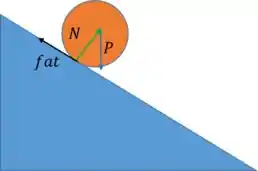
a)
Passo 2
b) Pela segunda lei de Newton, temos:
E então:
Substituindo na primeira equação:
E então:
Passo 3
c) Vamos analisar o caso onde , portanto:
Como , temos:
Resposta
a)
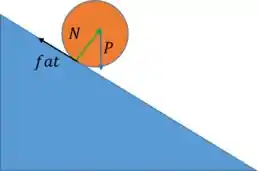
b)
c)
Exercícios de Livros Relacionados
Um mecanismo em forma de ioiô, montado em um eixo horizontal sem atrito, é usado para levantar uma caixa de 30kg , como mostra a figura abaixo. O raio externo R da roda é 0,5m e o raio r do cubo da ro
Na Fig. 11-60, uma força horizontal constante F → de módulo 12N é aplicada a um cilindro maciço homogêneo através de uma linha de pescar enrolada no cilindro. A massa do cilindro é 10k g , o raio é 0,
10.3E Um cilindro rola em uma rampa de inclinação θ = 30 ° . A) Calcule a aceleração angular do cilindro B) Calcule a força de atrito da rampa sobre o cilindro.
10.7P Calcule em termos do raio R da bola, o parâmetro de impacto b de uma tacada com que um jogador deve chutar uma bola para que esta tenha uma velocidade angular vertical dada por ω = v / 2 R .
Um ioiô possui um momento de inércia de 950 g c m ² ² e uma massa de 120 g . O raio do eixo é 3,2 m m e a corda tem 120 c m de comprimento. O ioiô rola para baixo, a partir do repouso, até a extremida