Uma esfera de massa e raio parte do repouso e rola sem deslizar sobre uma rampa que se encontra presa no solo. Essa rampa não é plana, como indica a figura, onde também está indicado que a esfera deixa a rampa no ponto , após seu centro de massa descer uma altura desconhecida. Observa-se que o centro de massa da esfera deixa a rampa com uma velocidade horizontal de módulo e que ela atinge um solo a uma distância da base da rampa. Desconsidere o efeito da resistência do ar com a esfera e use que o momento de inércia da esfera em relação a um eixo que passa pelo CM é . Considere que a esfera não perde o contato com a rampa até atingir o ponto .

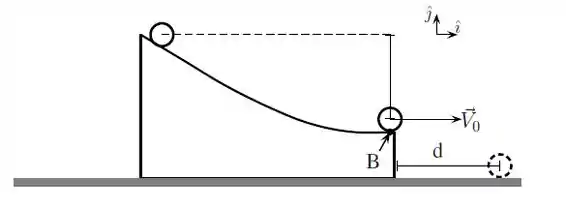
a) Qual é a diferença de altura do centro de massa da esfera entre o instante em que ela foi abandonada e aquele em que ela perde o contato com a rampa, no ponto ?

b) Qual é o trabalho realizado por cada uma das forças que atuam sobre a esfera no deslocamento do item (a)?

c) Qual é a altura do ponto em relação ao solo?

d) Usando os vetores unitários definidos na figura, determine o vetor velocidade do centro de massa da esfera no instante imediatamente anterior a atingir o solo.

e) Qual é a velocidade angular da esfera no instante de item (d)

Como a esfera parte do repouso, temos que:

Já quando ela perde o contato, há duas energias cinéticas na esfera, a de translação e a de rotação.

Temos que:

E:

Logo:

Voltando para a primeira expressão:

Temos:

b) Como dito antes, a única força que realiza trabalho é a força peso, portanto:

Logo:

c) Depois que perde o contato com a rampa, a esfera se desloca horizontalmente uma distância , certo? Com isso nós podemos encontrar o tempo de voo da esfera:

Com o tempo, podemos encontrar a altura que ela caiu depois de sair da rampa:

Como esta conta foi feita utilizando a esfera como uma partícula com a massa concentrada no centro de massa da esfera, precisamos somar o raio da mesma para encontrar a distância correta do ponto ao solo:

d) Como não há aceleração na horizontal no lançamento, a velocidade horizontal se mantém, portanto:

Já para encontrarmos a velocidade na vertical, usaremos a equação da velocidade do MRUV, com somente a gravidade como aceleração:

Portanto:

e) Depois de perder o contato com a rampa a única força sobre a esfera é a força peso. Como o peso atua no centro de massa da esfera, seu torque é zero. Como o torque no percurso de até o solo é nulo, temos que a velocidade angular é conservada.

Então para saber a velocidade angular da esfera imediatamente antes de chegar ao solo basta calcular a velocidade angular no ponto

Quando a esfera está no ponto , ela está rolando sem deslizar, então sua velocidade angular é dada por: