Um disco de raio e massa desce sem deslizar, a partir do repouso, a rampa inclinada conforme a figura. Após chegar à base da rampa , ele segue na horizontal para a pista em forma de circunferência com raio e sobe essa pista rolando sem deslizar. O ângulo entre a rampa e a horizontal é . O raio do disco vale e o comprimento da rampa, do ponto ao ponto , vale , onde é o raio da pista circular. A aceleração da gravidade local é . A linha tracejada corresponde a uma possível trajetória do centro de massa do disco.
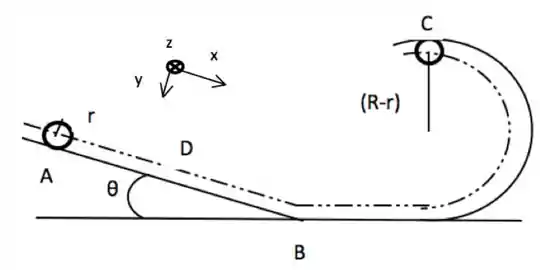
Faça o diagrama de forças para o disco durante o percurso de até . A partir das leis sobre torque e força, obtenha uma expressão literal, em função de , para o valor da aceleração do do disco entre e . Use o sistema de coordenadas desenhado na
figura.
Indique claramente o sentido da força de atrito estática feita pela superfície da rampa sobre o disco. Determine uma expressão literal para , em função de e . Resolva através da segunda lei de Newton aplicada ao centro de massa do disco.
Encontre uma expressão literal para o valor da velocidade angular do disco em
torno de um eixo horizontal que passe em seu , quando o disco chega ao ponto , em
função de e . Resolva através do uso de leis físicas referentes à energia mecânica.
O valor mínimo da velocidade do do disco para passar no ponto mais alto da
pista circular , sem perder o contato com a pista, é .
Obtenha uma expressão literal para a velocidade do do disco no ponto , , em
função de e através de leis físicas sobre a energia mecânica. Compare com o valor
mínimo dado e diga se o disco passará pelo ponto em contato com a pista ou se descolará dela antes de chegar a .
Passo 1
Vamos primeiro determinar as forças que atuam:
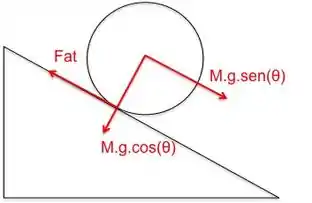
Agora podemos determinar as equações do movimento rotacional! Como usaremos o módulo, fique atento à regra da mão direita para verificar se os sinais estão corretos!
Para o movimento translacional, temos:
Substituindo o valor da força de atrito na equação com movimento rotacional, temos:
Isolando a aceleração do centro de massa e substituindo , fica:
Passo 2
Como já calculamos a equação do movimento translacional, temos:
Substituindo o valos da aceleração pelo que achamos no item , temos:
O sentido está indicado na figura do item !
Passo 3
Para determinar a velocidade angular do disco no ponto , vamos recorrer à conservação da energia mecânica, Olha só!
Como o objeto parte do repouso, antes ele possui apenas energia potencial gravitacional! Depois ele possui apenas energia cinética rotacional e translacional. Ou seja:
Como o disco rola sem deslizar, temos !
Isolando a velocidade angular, temos:
Substituindo , fica:
Passo 4
Para determinar a velocidade do centro de massa no ponto , vamos novamente recorrer à conservação da energia mecânica!
Ahh..estamos conservando energia do ponto para o ponto !
Substituindo por, temos:
Simplificando, temos:
Substituindo e :
Isolando a velocidade, temos:
Como a velocidade encontrada é maior do que a mínima necessária, o disco não descolará antes de chegar a .
Resposta