Considere o sistema abaixo, onde um cilindro maciço de massa e raio pode girar sem atrito em torno de um eixo vertical fixo à superfície, que passa pelo seu centro de massa. Uma corda ideal e de massa desprezível está enrolada em torno do cilindro, passa por uma polia em forma de aro com massa e raio e está presa a um bloco de massa desconhecida. Não há atrito nos eixos da rotação da polia e do cilindro e não ocorre escorregamento da corda no cilindro ou na polia. Tampouco há atrito entre o bloco e a superfície do plano inclinado. O raio da polia (aro) vale e o ângulo é . Observa-se que o bloco desce com uma aceleração linear .
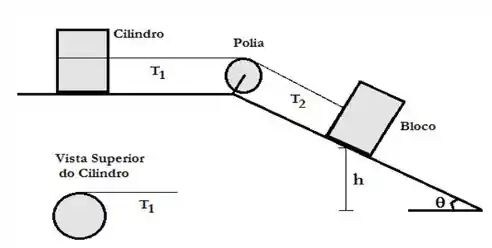
Havendo o sistema partido do repouso, observa-se que a polia sofre um deslocamento angular total de radianos até que o bloco chegue à base da rampa. Determine o tempo de queda do bloco, , e a velocidade angular final do cilindro maciço, .
Faça o diagrama do corpo livre para cada componente do sistema, representando claramente as forças que agem em cada um dos componentes e o sentido de seus movimentos (de translação ou rotação).
Escreva as equações resultantes das Leis de Newton (rotacional e translacional) para
os três corpos.
A partir das equações da letra , determine o valor da massa do bloco, em termos
de .
Passo 1
Para determinar o tempo de queda do bloco, vamos primeiro descobrir quanto de corda foi necessário para que ele chegasse até a base, ou seja, o quanto ele percorreu até chegar lá!
Como sabemos que o bloco partiu do repouso, e que possui aceleração , temos, de acordo com a cinemática:
Isolando o tempo, temos:
Passo 2
Para determinar a velocidade angular do cilindro, precisamos determinar quantos radianos ele girou para fornecer de corda. Pois, como temos o tempo que ele levou para fazer isso, teremos a velocidade angular! Se liga!
Agora é só calcular a velocidade angular:
Passo 3
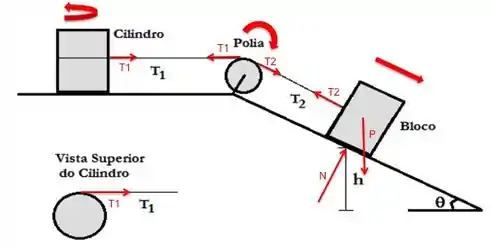
O cilindro e a Polia possuem movimento de rotação no sentido horário.
O bloco possue movimento de translação para baixo da rampa.
Passo 4
Para o cilindro, temos apenas movimento de rotação, portanto, a equação do movimento é:
Passo 5
Para a polia, temos:
Passo 6
Para o bloco, temos apenas movimento translacional, portanto, temos a seguinte equação:
Como o bloco possui massa desconhecia, utilizaremos para designá-la!
Passo 7
Para determinar o valor da massa do bloco, iremos somar as equações achadas no item , de modo a cancelar os valores desconhecidos!
isolando m, temos:
Substituindo os valores dados:
Resposta