Considere uma esfera que rola sem deslizar sobre uma calha simétrica que tem dois trechos retilíneos, I e II, como mostra a figura. Ela oscila descendo e subindo nos dois ramos da calha. No trecho I a força de atrito é e no trecho II, é . Considere que as únicas forças que atuam sobre a esfera sejam a força normal e a força de atrito exercidas pela calha, e o seu peso.
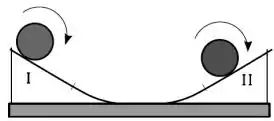
Dentre os diagramas seguintes:
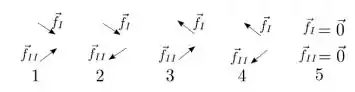
o que melhor representa o sentido e a direção das forças de atrito e nos trechos I e II é:
- 3
- 1
- 2
- 4
- 5
- Nenhuma das alternativas
Passo 1
Temos aqui uma esfera que rola sem deslizar e precisamos encontrar a força de atrito que atua nela.
Para uma esfera rolando sem deslizar em um plano inclinado, teremos um diagrama do corpo livre dessa forma:
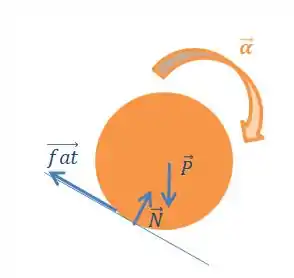
Vemos no diagrama acima, que a força de atrito é a única força capaz de realizar torque e é ela que irá gerar a aceleração angular representada acima.
E precisamos ficar atentos aqui numa coisa!
Não importa se a bola está subindo ou descendo o plano. A aceleração angular será sempre de forma que irá desacelerar a esfera se ela estiver subindo e que irá acelerar se ela estiver descendo.
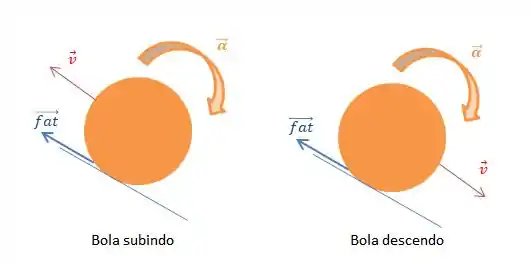
Faz sentido, né? Se você lança uma bola em direção a um plano inclinado, ela vai subir freando até parar e depois vai descer acelerando.
Então, é só pensarmos que a força de atrito estará sempre na direção subindo o plano!
Passo 2
Na rampa , teremos a seguinte configuração:
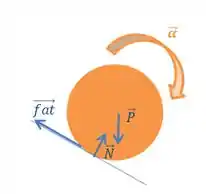
Portanto, o diagrama correto para a força de atrito nesse caso é:
![]()
E para a rampa , teremos a seguinte configuração:
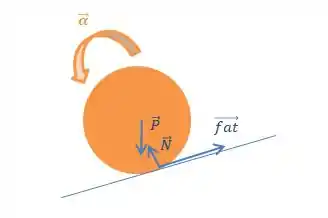
E o diagrama correto para a força de atrito é:
![]()
Sendo assim, a alternativa correta é a letra a), que representa o diagrama 3.
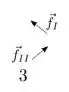
Resposta
- 3