Um cilindro de raio e massa é puxado por uma força horizontal de módulo em uma superfície também horizontal, por onde rola, sem deslizar. Sabendo que os coeficientes de atrito estático e cinético entre o cilindro e a superfície são, respectivamente, e ,
qual o trabalho realizado pela força de atrito em uma volta completa do cilindro?
Passo 1
O pulo do gato para entender essa questão está na na parte “[...]rola, sem deslizar.” Parece tentador escolher uma das fórmulas bonitas da questão, não é mesmo? Mas dá uma olhada nisso:
A formula acima parece complicada mas na verdade ela nada mais é do que a velocidade total de um ponto qualquer da casca cilindro em função da distância desse ponto pro eixo de rotação.
Mas caramba, onde vamos usar essa fórmula? Relaxa que dela, só precismos entender que a velocidade é depende da contribuição de dois fenômenos: o rolamento (parcela ) e a translação (velocidade do centro de massa ). Considerando um ponto sobre a circunferência (), temos o seguinte movimento:
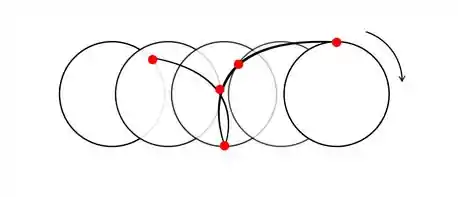
No ponto de contato com o chão, a velocidade total é nula porque a velocidade de cada um dos dois fenômenos tem mesmo módulo e direção mas veja: sentidos opostos! Isso significa que nesse ponto de contato não pode haver atrito cinético. Logo o trabalho da força de atrito deve ser nula, beleza?