Parte I:
Uma esfera sólida uniforme de massa e raio é colocada no lado de dentro de uma bacia hemisférica de raio . Existe atrito entre a esfera e a bacia. A esfera é liberada a partir do repouso fazendo um ângulo com a vertical, conforme ilustra a figura, e passa a rolar sem deslizar. A aceleração da gravidade é .
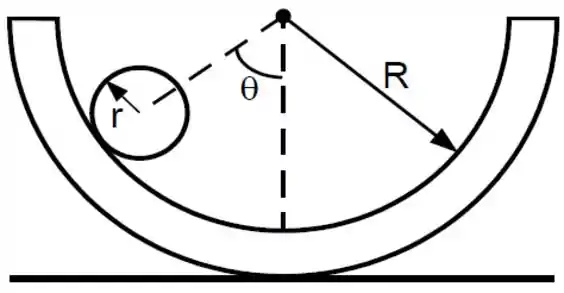
a) Expresse a conservação da energia do sistema.
b) Determine o módulo da velocidade angular da esfera quando ela atinge a parte inferior da bacia.
Parte II:
As setas no desenho abaixo, indicam as forças de atrito correspondentes à três posições da esfera quando ela está rolando sem deslizar no sentido horário. Assinale qual das opções é a verdadeira.
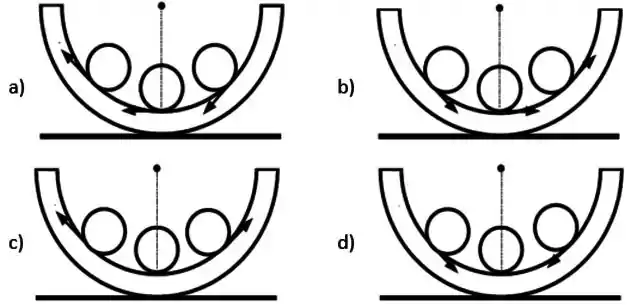
Passo 1
Parte I
a)
Pela conservação da energia mecânica,
E a única força não-conservativa agindo na esfera é a força de atrito, no ponto de contato da esfera com a bacia. Aí que tem que ficar atento! Ele disse que a esfera rola sem deslizar, e isso significa que o ponto de contato da esfera com a bacia tem velocidade nula: o atrito é estático.
E um detalhe importante da força de atrito estático é que ela não realiza trabalho! Pro ponto que está em contato com a bacia, é como se a esfera estivesse parada, então não há trabalho.
Passo 2
Portanto,
A energia mecânica é a soma da energia cinética com a energia potencial .
Aqui temos um movimento de translação e de rotação, então temos que considerar a energia cinética de translação e a energia cinética de rotação .
E a energia potencial vai ser somente gravitacional, , não tem nenhum mola ou força elástica que gere energia potencial elástica.
Ou seja, a equação de conservação de energia do sistema é:
Passo 3
b)
Ele quer a velocidade angular da esfera quando ela chega na parte de baixo da bacia. É claro que vamos usar a relação que acabamos de achar na letra (a)!
Sendo o momento inicial e o momento final, isso dá:
Então o objetivo dessa questão é achar o .
Passo 4
Vamos ver o que que dá pra ajeitar!
Primeiro, como a esfera parte do repouso, suas velocidades iniciais, escalar e angular, são nulas:
Conforme a gente for achando os valores das variáveis, eu vou atualizando a nossa equação, beleza?
Então ficou:
Passo 5
Outra coisa: podemos usar a relação
Ou seja,
É uma boa, já que queremos achar !
Então a nossa equação vai ser:
Passo 6
O momento de inércia de uma esfera de massa e raio é:
Logo, a equação atualizada é:
Passo 7
Agora vamos calcular a altura inicial da esfera em relação ao fundo da bacia. Pra isso vamos apelar pra uma trigonometria.
Observação: a altura diz respeito ao centro de massa da esfera, que fica bem no meio dela.
No momento que a esfera é liberada, temos a seguinte situação:
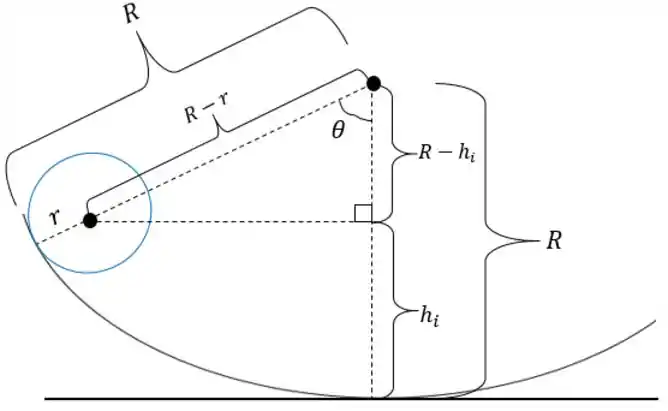
Logo,
Passo 8
Show! Então só falta a altura final . E ela vai ser simplesmente o raio da esfera, saca:
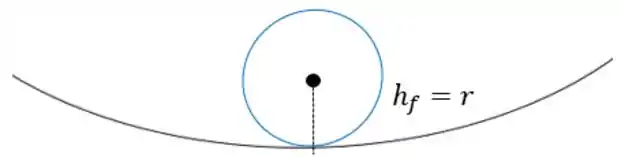
Passo 9
Ou seja,
Passo 10
Ótimo! Então nossa equação da conservação da energia ficou:
Pronto! , , , e nós conhecemos, então a única variável desconhecida é .
Agora é arregaçar as mangas e fazer as contas! Vamos ter:
Deu um valor bem bizarro mas é isso mesmo! :)
Passo 11
Parte II
Como já vimos láá atrás, a força de atrito entre a esfera e a bacia é de atrito estático, porque a esfera rola sem deslizar. A velocidade no ponto de contato entre a esfera e a bacia é nula.
Então temos que olhar pras figuras pensando nisso. Pra facilitar a visualização, a gente pode imaginar que a esfera está parada!
Passo 12
O chão no lado esquerdo da bacia é inclinado pra direita, então se a esfera estivesse lá parada, ela teria tendência a cair pra direita, então pra esfera se manter em repouso a força de atrito tem que ser pra esquerda:
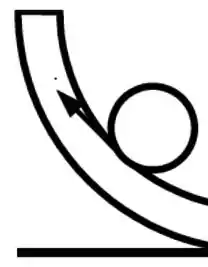
A explicação mais formal seria dizer que a resultante das que atuam na esfera (peso e normal) aponta pra direita, então pra esfera estar em repouso a força de atrito tem que apontar pra esquerda.
Passo 13
Usando o mesmo raciocínio do outro lado, temos:

Passo 14
E no meio, lá embaixo da bacia, o chão é horizontal, então a força peso e a força normal se cancelam totalmente. Logo, pra esfera se manter em repouso, a força de atrito tem que ser nula:
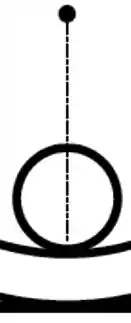
Portanto, a alternativa correta é a letra (c)!
Resposta
Parte I:
a)
b)
Parte II:
Alternativa (c)