Um disco de massa e raio está em repouso sobre uma superfície plana, horizontal e com atrito. Num dado instante aplica-se no seu centro uma força constante, cuja direção faz um ângulo com a horizontal, como mostra a figura. Sabe-se que o disco rola sem deslizar sobre a superfície e que o momento de inércia do disco em relação a um eixo perpendicular ao plano do disco e que passa pelo seu centro é .
Considere a resistência do ar desprezível, e que a gravidade tem módulo conhecido.
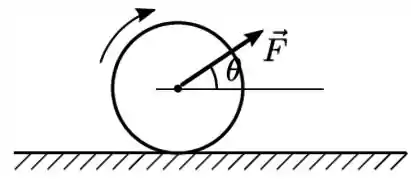
a) Faça um diagrama representando todas as forças que agem sobre o disco nos seus respectivos pontos de aplicação.
b) Determine o módulo da aceleração, , do centro de massa do disco enquanto ele se desloca.
c) Determine o módulo e o sentido da força de atrito que atua sobre o disco.
d) Determine a energia cinética adquirida pelo disco no instante em que dá uma volta completa a partir do instante inicial.
Passo 1
a)
Vamos começar identificando as forças que atuam no disco!São:
- seu peso , que age pra baixo e no centro do disco (centro de massa)
- a força normal da superfície , que age pra cima, no ponto de contato do disco com a superfície
- a força de atrito , que também atua no ponto de contato do disco com a superfície. Já a direção da força de atrito é um problema, por enquanto não tem como saber, por causa dessa mistura de rotação e translação. Vamos assumir que ela aponta pra esquerda e qualquer coisa depois a gente troca, beleza?
- e claro, a , que age no centro do disco, fazendo um ângulo com a horizontal.
Passo 2
Então o diagrama de forças é:
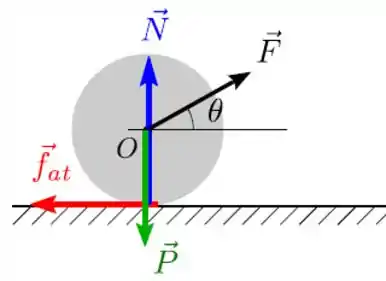
Passo 3
b)
Quando temos situações como essa, de rolamento sem deslizar e com várias forças atuando, temos que montar equações a partir da 2ª lei de Newton:
e pra rotação:
Passo 4
Mas a força não tá legal fazendo um ângulo com a horizontal. Por isso vamos decompô-la em uma componente paralela à superfície e uma componente ortogonal à superfície.
Com uma trigonometriazinha básica, obtemos a decomposição:
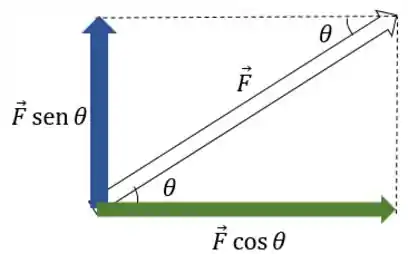
Passo 5
Agora sim podemos aplicar a 2ª lei de Newton!
Vamos focar primeiro no eixo paralelo à superfície. As forças atuando nesse eixo são , pra direita, e , pra esquerda. Então, vamos ter:
O disco se movimenta pra direita, então em módulo a equação fica:
Vou ir numerando essas equações que a gente vai achar, que nem essa que eu chamei de .
Passo 6
Agora vamos ver o que acontece no eixo perpendicular à superfície.
As forças atuando nesse eixo são e , pra cima, e , pra baixo. E não há movimento nesse eixo, então essas forças se cancelam:
Ou, em módulo:
E , então:
Passo 7
Show, agora vamos analisar a rotação!
Repare que a única força que produz torque em relação ao eixo passando pelo centro de massa do disco é a força de atrito .
Pois é, a e a atuam diretamente no CM, enquanto o vetor posição da normal é paralelo a ela mesmo, então nenhuma dessas realiza torque!
Logo,
Passo 8
A força de atrito atua a uma distância do centro do disco, então o torque da força de atrito tem módulo
Logo,
Passo 9
E no rolamento sem deslizar, ainda temos a condição de vínculo .
Então junto isso tudo, obtemos o sistema:
Passo 10
Pela equação , temos
E pela equação ,
Juntando esses valores na equação , obtemos:
Passo 11
Lembrando que , isso dá:
Cortando dos 2 lados:
Deu um bom trabalho, mas conseguimos achar a aceleração! :D
Passo 12
c)
Agora ficou fácil de achar a o módulo da força de atrito, a gente já montou as equações todas!
Vimos que
Ou seja,
Passo 13
Agora vamos ver se isso condiz com o sentido que a gente determinou antes pra força de atrito, pra esquerda.
Pela figura, podemos ver que
Logo,
Então módulo da força de atrito é positivo, e um módulo tem que ser que ser positivo mesmo né! Isso significa que o sentido que escolhemos pra força de atrito estava certo.
Passo 14
d)
Vamos aplicar o teorema trabalho-energia cinética! Ele diz que o trabalho total é igual à diferença de energia cinética :
Passo 15
Depois de uma volta completa, o deslocamento do centro de massa do disco é igual ao seu perímetro, ou seja . Então o deslocamento que a gente tem que considerar na hora de calcular o trabalho é esse .
Passo 16
Vejamos, as forças peso, normal e são perpendiculares ao movimento, então elas não realizam trabalho. E na verdade, a força de atrito também não, porque no rolamento sem deslizar, o atrito é estático (a velocidade do ponto de contato com o chão é nula). E o atrito estático não realiza trabalho: sem deslocamento não tem como haver trabalho!
Ou seja, a única força que realiza trabalho no disco é a força :
Passo 17
E a é constante e aponta no sentido do movimento, então esse trabalho é:
Passo 18
Portanto, voltando pro teorema trabalho-energia cinética:
A é a diferença da energia cinética (que a gente quer achar) e da energia cinética inicial . Mas o bloco parte do repouso, então . Logo, .
Ótimo! Então a energia cinética final é:
Resposta
a)
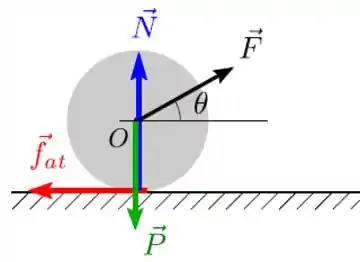
b)
c)
d)