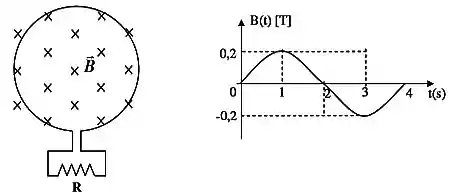
O circuito abaixo é composto de uma resistência () e uma espira circular (área ). A espira circular se encontra imersa em uma região do espaço que contém um campo magnético aplicado perpendicular a sua área (o sentido do campo é entrando no papel). Considere que a intensidade do campo varia no tempo conforme o gráfico abaixo e calcule para e segundos:
- O sentido da corrente induzida na espira.
- O valor da corrente induzida.
Passo 1
Vamos lá, então, calcular o sentido da corrente induzida! Essa é mole e nós precisamos do cérebro e da mão direita.
Para , o campo magnético está aumentando (consegue ver no gráfico que ele aumenta a partir da origem do gráfico?). Então, o campo induzido estará ao contrário do campo aplicado, ou seja, para fora da folha. Aplicamos a regra da mão direita e pimba!, a corrente está no sentido anti horário.
Para , o campo magnético está diminuindo no tempo. O campo induzido, então, está no mesmo sentido do campo aplicado, ou seja, para dentro da folha. De novo usamos a regra da mão direita e pimba!, a corrente está no sentido horário.
Para , o campo magnético não se altera. Como saber isso? Trata-se do valor mínimo, do vértice da função, onde a derivada é nula. E qual é a derivada?
Não tem fluxo, logo a corrente induzida é nula.
Passo 2
Agora precisamos calcular o valor das correntes induzidas.
Sabemos que o cálculo da corrente induzida é dada por:
Então precisamos achar o fluxo para calcular a fem induzida:
Pelo gráfico, trata-se de uma função senoidal. Calculamos a variação do fluxo por:
Também pelo gráfico, sabemos que o período é , logo
Como o campo magnético é homogêneo,
Voltamos, agora, pra fem induzida:
E por fim, a corrente induzida.
Resposta
- Para , corrente no sentido anti horário.
Para , corrente no sentido horário.
Para , não há corrente.