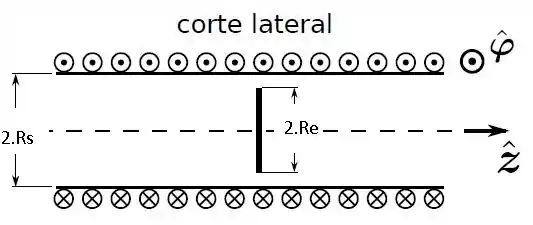
Um solenoide ideal, com voltas por unidade de comprimento (axial) e seção transversal circular de raio , é percorrido por uma corrente elétrica cuja intensidade varia no tempo de acordo com (). Dentro do solenoide, em um plano perpendicular ao seu eixo, com raio , coloca-se uma espira circular condutora de resistência . A autoindutância da espira e a indutância mutua entre essa e o solenoide são desprezíveis. Considere, ademais, que a lei de Ampére usual possa ser aplicada.
- Determine o vetor campo magnético dentro do solenoide, produzido pela corrente .
- Qual é a intensidade da corrente induzida na espira?
- Qual é o sentido de tal corrente induzida?
- Determine o vetor campo elétrico induzido na espira.
Passo 1
Como eles inventaram essa rataria de poder fazer Ampère clássica com a corrente variando, é justamente o que nós vamos fazer:
Escolhendo uma Amperiana retangular de dimensões e :
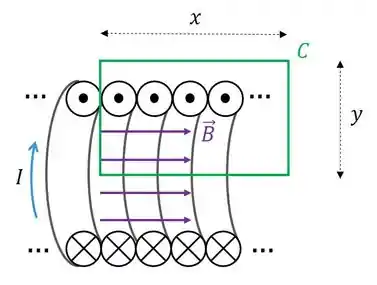
Passo 2
Temos que o campo é nulo fora do solenoide, além de que o produto escalar ser nulo nos lados :
No lado que está dentro do solenoide temos:
Temos o módulo do campo constante ao longo de todo o segmento retilíneo:
Passo 3
Agora determinamos a corrente que atravessa a nossa Amperiana. Se tivermos fios dentro dela, a corrente total será:
Pois cada um passa de corrente. Substituindo tudo:
Utilizando o dado do enunciado, que é o número de espiras por unidade de comprimento:
Além disto, pela regra da mão direita o vetor aponta no sentido de :
Passo 4
A intensidade da corrente induzida pode ser encontrada pela Lei de Faraday junto à Lei de Ohm:
Segue que:
Passo 5
Agora precisamos determinar a variação do fluxo magnético. Pela fórmula de fluxo:
Orientamos a área no sentido do campo:
Fazemos o produto escalar:
E integramos:
Temos que a área é :
Passo 6
Derivando o fluxo com respeito ao tempo e plugando na fórmula:
Sabemos que a corrente é :
Temos então nossa corrente induzida. A intensidade pode ser obtida tirando o módulo.
Passo 7
Pela Lei de Lenz, como temos um fluxo magnético aumentando no sentido de :
Temos que a corrente induzida vai tentar se opor à esse efeito. Por conta disto, ela vai ficar no sentido horário se olharmos para :
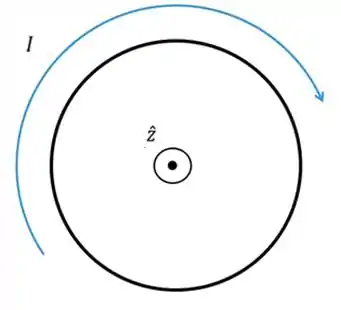
Passo 8
Agora vamos encontrar o vetor campo elétrico. Nós obtivemos a força eletromotriz por Faraday:
Pela definição da força eletromotriz podemos encontrar o campo elétrico:
Substituindo:
Como o campo elétrico é quem puxa a corrente, ele vai ter um aspecto circular por conta do formato do circuito. Podemos então rodar uma espécie de Lei de Ampère, lembrando que a orientação da curva já está fixada uma vez que tenhamos determinado o sentido do vetor área.
Passo 9
Pelo que argumentamos, o campo vai ser tangente ao circuito em todos os pontos:
Sim, dá negativo. O vetor área aponta no sentido de conforme estipulamos, já o campo fica no sentido da corrente. Por conta disto nosso e são paralelos mas em sentidos opostos.
Continuando... Pela simetria do problema (quando não souber o que falar, diga a palavra “simetria”) vamos ter o módulo do campo elétrico constante em todo o circuito:
Segue que o módulo do campo elétrico vai ser:
Como sabemos que ele gira no sentido da corrente, pela regra da mão direita ajustamos:
Atenção pro sinal. O sentido de é obtido colocando o polegar no sentido de e os outros dedos vão dar o sentido do giro positivo.
Resposta
a)
b)
c)
Sentido horário se olharmos para .
d)