Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Lei de Lenz

Ver Teoria
Exercício 97123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596

Enunciado

UFRJ- Física 3 – SC 2018.1 - DIURNO - 4

Considere um anel circular condutor, situado no plano X Y e centrado na origem, imerso em um campo magnético uniforme   B → , como mostrado na figura abaixo. O anel então é aquecido, de modo que o seu raio varia no tempo como R t = R 0 ( 1 + a t ) , onde R 0 e a são constantes positivas. Além disso, o campo magnético também varia no tempo como   B → t = b t 2 z ^ , onde b também é uma constante positiva.

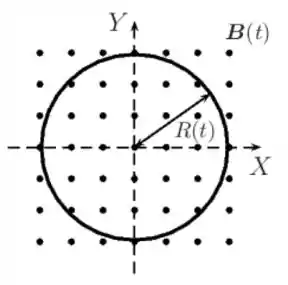
  1. Determine o fluxo magnético através da área definida pelo anel em um instante t > 0 .
  2. Determine a intensidade e o sentido da força eletromotriz induzida no anel no mesmo instante.

Passo 1

Vamos primeiro tentar entender o que está acontecendo aqui. Como o raio do anel está aumentando com o tempo, a área através da qual o campo magnético passa também está variando com o tempo. Além disso, a intensidade esse campo magnético também está aumentando com o tempo.

Com isso, o fluxo magnético aumenta com o tempo por duas razões combinadas: o campo magnético aumenta com o tempo e ele atravessa uma área cada vez maior com o tempo. Por isso, vai aparecer uma fem induzida que vai se opor à variação temporal desse fluxo.

Passo 2

a) Agora, o problema diz para nós que o campo magnético é uniforme, o que significa que ele tem o mesmo valor em todos os pontos do espaço para cada instante de tempo t . Então fica ligado, vamos repetir essa ideia com cuidado:

“   A   i n t e n s i d a d e   d o   c a m p o   a u m e n t a   c o m   o   t e m p o ,   m a s   p a r a   t o d o   i n s t a n t e   t   ,

                                                        e s s a   i n t e n s i d a d e   é   i g u a l   e m   t o d a   a   r e g i ã o   d o   e s p a ç o . ”

Essa observação é muito importante, pois é isso que nos permite tirar o vetor  B → ( t ) da integral do fluxo magnético Φ B ( t ) através da área S e escrever o seguinte:

Φ B ( t ) = ∫ S B → t ⋅ d A → t = B → ( t ) ⋅ ∫ S d A → t = B → t   .     A → S ( t )   ,

mostrando o produto escalar entre B → ( t ) e A → S ( t ) , e A → S t é o vetor área que é perpendicular ao plano da página.

Para continuar, vamos colocar  A → S t no mesmo sentido do campo magnético, ou seja:

A → S ( t ) = π R t 2 ( + z ^ )   .

Assim, A → S ( t ) é paralelo ao campo  B → ( t ) e o fluxo magnético pode ser simplificado para:

Φ B t = b t 2   π R t 2     ⇒       Φ B t = b π R 0 2 1 + a t 2   t 2     ,  

que mostra, explicitamente, que o fluxo magnético aumenta com o tempo, uma vez que b > 0 .

Passo 3

b) Pela lei de Faraday, a força eletromotriz induzida no anel é dada por:

E i n d = - d Φ B t d t = - b π R 0 2 1 t 2 d d t 1 + a t 2 + 1 + a t 2 d d t 1 t 2     ,

que podemos simplificar um pouco mais realizando as derivadas

E i n d = - b π R 0 2 1 t 2   2 a 1 + a t + 1 + a t 2 - 2 t 3

= - 2 b π R 0 2 1 + a t a t - 1 - a t t 3   ,

que por fim, resulta em:

E i n d = 2 b π R 0 2 ( 1 + a t ) t 3 > 0   ,

já que a , b são constantes positivas.

Note que a fem é positiva para qualquer t > 0 , o que implica que o seu sentido corresponde ao sentido positivo dado pela regra da mão direita a partir do vetor unitário normal ao plano do anel, que é   z ^ . Este sentido é anti-horário. Este resultado também pode ser inferido a partir da lei de Lenz, notando que, embora a área do anel esteja crescendo com o tempo, a intensidade do campo magnético está caindo mais rapidamente, de forma que o fluxo está decrescendo com o tempo . Para compensar esta variação, a corrente induzida deve produzir um campo cuja componente z tenha o mesmo sentido de   B → , o que corresponde ao sentido anti-horário.

Resposta

  1. Φ B t = b π R 0 2 1 + a t 2   t 2   ;
  2. E i n d = 2 b π R 0 2 ( 1 + a t ) t 3 > 0 : sentido anti-horário.

Exercícios de Livros Relacionados

20- Uma barra metálica com 1.50m de comprimento é puxada para a direita a 5.0m / s regulares e perpendicularmente a um campo magnético uniforme de 0.750T . A barra desliza sobre trilhos metálicos para
17- Use a lei de Lenz para determinar o sentido da corrente induzida que passa no resistor a b indicado na Figura 29.33 , quando ( a ) a chave S é aberta depois de ficar fechada durante alguns minutos
15- Um anel circular está em uma região do espaço onde existe um campo magnético uniforme, como indica a Figura 29.31 . O campo magnético está entrando no plano da figura. Determine o sentido (horário
18- Um tubo de papelão é circundado por dois enrolamentos feitos com dois fios isolados, formando espiras em sentidos contrários, como indica a Figura 29.34 . Os terminais a e b do enrolamento A podem
16- A corrente na Figura 29.32 obedece a equação I t = I 0 e - b t . Em que b0 . Determine o sentido (horário ou anti-horário) da corrente induzida na bobina redonda para t0 .