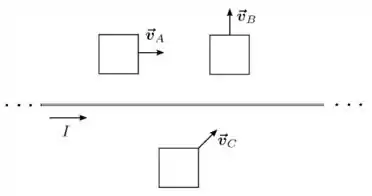
Um fio fino, retilíneo e infinito transporta uma corrente estacionária de intensidade , no sentido indicado na figura abaixo. Três espiras quadradas, , e , posicionadas no mesmo plano do fio e com dois de seus lados paralelos ao mesmo, se movem com velocidade constante nos sentidos indicados, preservando as suas orientações. As espiras e são condutoras, enquanto a espira é isolante. Responda, justificando cada resposta:

1. Haverá corrente induzida sobre a espira ? Se sim, indique o seu sentido.
2. Haverá força eletromotriz induzida sobre a espira ? Se sim, indique o seu sentido.
3. O fio exercerá força magnética sobre a espira ? Se sim, indique o seu sentido.

b) Diferente do caso anterior, a espira com velocidade  caminha numa direção perpendicular ao fio infinito e, por isso, as posições de seus pontos ao fio serão diferentes à medida que o tempo passa. Nesse caso, então, haverá um fluxo magnético que vai variar com tempo e, consequentemente, também haverá fem induzida, embora o espira seja feita de material isolante!

CUIDADO: o fluxo magnético varia com tempo, já que depende apenas da variação do campo através da área da espira, mas não aparece corrente induzida porque o material da espira é isolante.

Para encontrarmos o sentido dessa fem induzida, podemos utilizar a lei de Lenz: como o fluxo magnético está diminuindo com o tempo à medida que a espira se afasta, precisa haver um fluxo magnético que opõe a essa diminuição.

Portanto, deve aparecer uma fem induzida no sentido anti-horário.

c) A espira é condutora, então, caso haja uma fem induzida, vai aparecer também uma corrente induzida. É importante ficar ligado nesta ideia: para ter fem induzida, basta que o fluxo do campo magnético varie com o tempo, e isso independe do tipo de material de que é feito a espira! Mas vamos analisar o caso da espira condutora , que tem uma velocidade inclinada com relação ao fio.

Como vimos no Passo 1, o fluxo magnético através da espira não varia com o tempo porque ela tem velocidade paralela ao fio. Por isso, no caso da espira , basta a gente olhar para a componente de   perpendicular ao fio.

Como a espira se aproxima do fio, o campo magnético aumenta com o tempo, já que as distâncias dos pontos da superfície da espira ao fio estão diminuindo com o tempo. Então, vai haver um fluxo magnético que aumenta com o tempo e por isso uma fem induzida e uma também uma corrente induzida.

c) Continuação...

Agora o que temos é uma espira percorrida por uma corrente na presença de campo magnético e isso dar origem a uma força magnética atuando nas arestas dessa espira. Essa força é dada por

Para analisarmos como fica a força sobre a espira, vamos dar uma olhada para a figura abaixo, que mostra a corrente induzida no sentido anti-horário e  produzido por entrando no plano da página e perpendicular a ela.

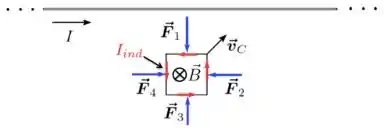
Nas arestas perpendiculares ao fio, as forças resultantes  e  sobre elas terão mesmo módulo, mesma direção, porém sentidos contrários, como está na figura acima. Basta, então, olhar para a força resultante atuando sobre as arestas paralelas ao fio, ou seja, precisamos ver como são as forças e  e depois somá-las vetorialmente para termos a força resultante.

Nestas arestas, a força sobre cada uma delas terá intensidade diferente, pois os campos magnéticos devidos a nas respectivas posições têm intensidades diferentes. No caso da aresta mais próxima ao fio, o campo é mais intenso e isso faz com a força  seja mais intensa do que a força , que tem sentido contrário a . Como resultado, a força resultante sobre a espira será perpendicular ao fio e se afastando dele.

Resumindo, a força sobre será perpendicular ao fio e se afastando dele.