Força e Torque sobre uma Espira, Lei de Biot Savart, Lei de Ampère, Lei de Faraday, Lei de Lenz
Considere um trilho condutor em forma de , ao lado de um fio infinito que transporta uma corrente estacionária , como indica a figura (onde indicamos ainda os vetores unitários das coordenadas cilíndricas , e ).
Suponha que uma haste metálica de comprimento é colocada entre os dois braços do trilho formando um circuito fechado, e que uma força externa faz a haste deslizar sobre o condutor com velocidade constante .
Despreze as forças de atrito e a resistência do trilho, e considere que a resistência da haste é igual a . Despreze ainda qualquer efeito auto indutivo e capacitivo.
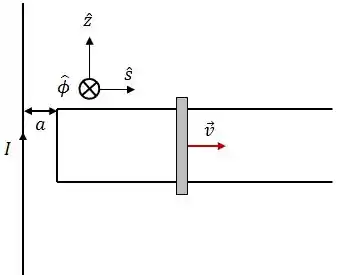
Qual a direção do campo magnético gerado pelo fio infinito, num ponto arbitrário? Argumente detalhadamente, utilizando seus conhecimentos de magnetismo e/ou argumentos de simetria.
Obtenha o módulo do campo magnético gerado pelo fio, num ponto arbitrário. Note que, dependendo do argumento utilizado, argumentos de simetria se farão necessários.
Calcule o fluxo magnético gerado pelo campo magnético do fio infinito no circuito (trilho + haste).
Determine o módulo e o sentido da corrente induzida no circuito. Novamente, argumente detalhadamente, utilizando seus conhecimentos de magnetismo.
Calcule a força magnética sobre a haste quando ela está a uma distância do fio infinito.
Passo 1
Qual a direção do campo magnético gerado pelo fio infinito, num ponto arbitrário? Argumente detalhadamente, utilizando seus conhecimentos de magnetismo e/ou argumentos de simetria.
Um dos modos que podemos utilizar para calcular o campo magnético gerado por um condutor é através da lei de Biot-Savart, dada por:
Onde tem a mesma direção e sentido da corrente.
Assim, pegando dois pontos aleatórios, um de cada lado do fio, os vetores e serão dados por:
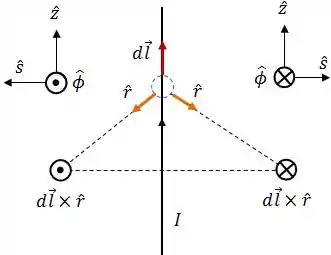
Portanto, o produto vetorial apontará sempre na direção e sentido do vetor , isso significa que o campo magnético também apontará na direção e sentido do vetor para qualquer ponto aleatório.
Passo 2
Obtenha o módulo do campo magnético gerado pelo fio, num ponto arbitrário. Note que, dependendo do argumento utilizado, argumentos de simetria se farão necessários.
Como se trata de um fio retilíneo infinito, podemos utilizar a lei de Ampère para determinar o módulo do campo magnético.
Devido a simetria do problema, a amperiana, nesse caso, será uma circunferência de raio , cujo eixo de simetria coincide com o fio.
Dessa forma, e , onde .
Finalmente:
Passo 3
Calcule o fluxo magnético gerado pelo campo magnético do fio infinito no circuito (trilho + haste).
O fluxo magnético é dado por:
A ideia é essa aqui:
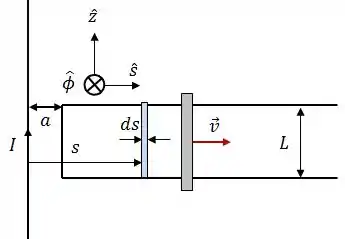
Daqui podemos tirar que:
Portanto:
Passo 4
Determine o módulo e o sentido da corrente induzida no circuito. Novamente, argumente detalhadamente, utilizando seus conhecimentos de magnetismo.
A corrente induzida está relacionada com a induzida através da relação:
Então vamos começar calculando a induzida através da lei de Faraday, dada por:
Onde .
Assim, a corrente induzida é dada por:
Passo 5
O sentido da corrente induzida é determinado através da Lei de Lenz, que diz:
O sentido de qualquer efeito de indução magnética é tal que ele se opõe à causa que produz esse efeito.
Resumindo, o que ela quer dizer é o seguinte:
Se o fluxo magnético estiver aumentando na espira, o campo magnético induzido vai estar no sentido contrário ao campo magnético externo.
Se o fluxo magnético estiver diminuindo na espira, o campo magnético induzido vai estar no mesmo sentido do campo magnético externo.
Vamos calcular, então, a taxa de variação do fluxo magnético:
Logo:
Isso significa que o campo magnético induzido vai estar no sentido contrário ao campo magnético externo, ou seja, o campo magnético induzido vai estar apontando para fora da página. Assim, de acordo com a regra da mão direita, a corrente deverá estar no sentido anti-horário.
Passo 6
Calcule a força magnética sobre a haste quando ela está a uma distância do fio infinito.
A força magnética sobre um condutor é dada por:
Mas como se trata de um fio retilíneo, a força magnética será dada por:
Onde tem a direção e sentido da corrente, logo, .
Assim, substituindo e , teremos:
Dando uma arrumada nesse cara, finalmente teremos:
Resposta
O campo magnético apontará na direção e sentido do vetor para qualquer ponto aleatório.
A corrente estará no sentido anti-horário.