Considere um solenoide infinito de raio com espiras por unidade de comprimento por onde passa uma corrente
onde é uma constante com dimensão de inverso de tempo.
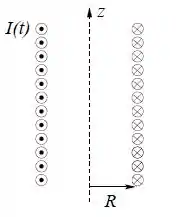
Dado: o vetor campo magnético do solenoide é .
Calcule o vetor campo elétrico no exterior do solenoide para .
Calcule o vetor campo elétrico no interior do solenoide para .
Considere uma partícula com carga e massa que, no instante , está parada a uma distância do eixo do solenoide conforme a figura. Calcule o vetor aceleração desta partícula em .
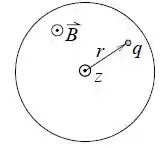
Corte transversal
Passo 1
Calcule o vetor campo elétrico no exterior do solenoide para .
Aqui vai ser necessário interligarmos alguns conhecimentos que temos sobre a matéria, beleza?
Bom, mesmo que a área transversal da região permaneça constante, a variação do campo magnético com o tempo vai gerar uma variação do fluxo magnético com o tempo, concorda?
De acordo com a lei de Faraday, a variação desse fluxo magnético vai gerar uma induzida, dada por:
Onde , logo:
Até aqui, tudo bem?
Agora é importante lembrar que nós podemos associar a induzida com o campo elétrico induzido através da relação:
Substituindo isso na lei de Faraday, teremos:
Agora sim, podemos seguir em frente.
Passo 2
Por conta da simetria do problema, , onde é tangencial à circunferência de raio e positivo no sentido anti-horário.
Para calcularmos o campo elétrico fora do solenoide, a curva através da qual vamos calcular o campo elétrico deve ter essa cara:
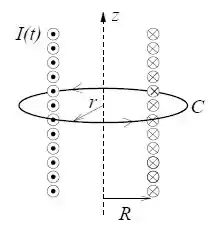
Portanto:
Obs.: A área por onde há fluxo magnético é apenas, nesse caso, a área que corresponde ao interior do solenoide, por isso .
De acordo com o problema, . Logo:
Finalmente:
Passo 3
Calcule o vetor campo elétrico no interior do solenoide para .
Aqui, a ideia é bem parecida com o que fizemos no passo anterior.
A diferença é que, agora, como queremos calcular o campo elétrico no interior do solenoide, a curva através da qual vamos calcular o campo elétrico deve ter essa cara:
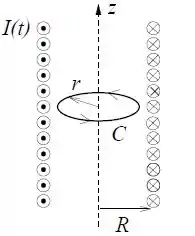
Agora, como estamos trabalhando com uma região menor que a seção reta do solenoide, vamos considerar o fluxo magnético somente pela região delimitada pela curva , beleza?
Portanto:
Passo 4
Considere uma partícula com carga e massa que, no instante , está parada a uma distância do eixo do solenoide conforme a figura. Calcule o vetor aceleração desta partícula em .
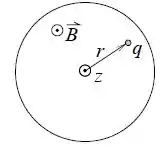
Nessa região, existem dois campos presentes, o campo magnético e o campo elétrico.
A força magnética sobre uma carga é dada por:
Ou seja, como a carga está parada, .
Passo 5
Assim, não precisamos nos preocupar com a força magnética sobre a partícula, restando apenas a força elétrica, dada por:
Como a carga está no interior do solenoide:
Logo:
Por último, podemos associar a força com a aceleração através da 2ª lei de Newton:
Finalmente:
Resposta