Indique com V se a afirmação é verdadeira, ou F, se falsa.
Uma partícula carregada pode ter um movimento retilíneo uniforme em uma região do espaço contendo campos elétrico e magnético uniformes, se eles forem perpendiculares entre si.
Quando uma espira condutora e outra isolante, ambas rígidas e em repouso, são posicionadas perpendicularmente a um campo magnético uniforme que varia no tempo, surge uma força eletromotriz induzida apenas na espira condutora.
Ao fazermos passar uma corrente estacionária através das espiras helicoidais de uma mola feita de material condutor, as espiras se aproximam, como se a mola fosse comprimida.
Em um fio condutor ôhmico dado, ao dobrarmos a diferença de potencial entre suas extremidades, dobramos sua resistência.
O fluxo do campo magnético da Terra através da superfície correspondente ao território brasileiro é igual, em módulo, ao fluxo do campo magnético da Terra através da superfície correspondente a todo o resto do globo terrestre.
A lei de Ampère afirma que, para correntes estacionárias, o fluxo do campo magnético através de uma superfície é igual a vezes a corrente que atravessa .
Uma espira retangular de metal, originalmente sem corrente, está próxima de um fio longo e retilíneo, que transporta corrente, com dois de seus lados paralelos ao fio. O fio e a espira se encontram no mesmo plano. Quando a corrente do fio está diminuindo, a espira é atraída pelo fio.
Para um condutor usual, como o cobre, o aumento da temperatura aumenta as vibrações moleculares, provocando maior espalhamento dos elétrons, o que faz com que sua resistividade diminua.
Se a circulação do campo magnético ao longo de um caminho fechado for nula, não haverá nenhuma partícula carregada em movimento atravessando uma superfície aberta delimitada pela curva que descreve esse caminho.
A força magnética sobre uma espira carregando uma corrente estacionária, localizada em uma região de campo magnético uniforme é sempre nula, independentemente do formato da espira.
Passo 1
Bom, vamos analisar uma afirmação por vez, beleza?
Uma partícula carregada pode ter um movimento retilíneo uniforme em uma região do espaço contendo campos elétrico e magnético uniformes, se eles forem perpendiculares entre si.
Esta situação é o que chamamos de “Campos Cruzados”. A ideia é basicamente essa, vamos imaginar aqui uma partícula de carga se movendo em uma região com campos elétrico (da direita para a esquerda) e magnético (entrando no plano da página) perpendiculares, um em relação ao outro.
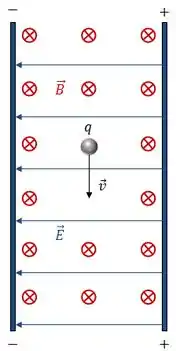
Neste caso irão surgir forças elétrica e magnética atuando sobre a carga, conforme mostrado abaixo.
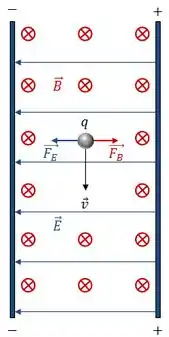
Se essas forças tiverem o mesmo módulo, elas irão se anular e a força resultante sobre a partícula carregada será nula e, por consequência, a partícula irá se mover em movimento retilíneo uniforme.
Logo, a afirmação é verdadeira.
Passo 2
Quando uma espira condutora e outra isolante, ambas rígidas e em repouso, são posicionadas perpendicularmente a um campo magnético uniforme que varia no tempo, surge uma força eletromotriz induzida apenas na espira condutora.
Vamos lá! As duas espiras são rígidas (logo, as áreas inscritas nas mesmas são constantes) e passa através delas um campo magnético perpendicular e que varia no tempo.
Se estamos falando de variação de campo magnético através de uma espira, estamos falando em variação do fluxo magnético, logo, estamos falando da Lei de Faraday, dada por:
Neste caso, com o campo magnético perpendicular às espiras rígidas, podemos escrever a equação acima como:
Opa! Repare que para calcular a fem induzida não levamos em consideração o material da espira. Logo, a fem induzida vai surgir nas duas espiras.
Assim, a afirmação é Falsa.
O material da espira seria relevante se estivéssemos falando em corrente induzida. Uma vez que a fem induzida surgirá em ambas as espiras, somente a espira feita de material condutor irá conduzir corrente.
Passo 3
Ao fazermos passar uma corrente estacionária através das espiras helicoidais de uma mola feita de material condutor, as espiras se aproximam, como se a mola fosse comprimida.
Se olharmos a seção da mola (para apenas duas espiras), teremos uma representação da corrente elétrica mais ou menos assim:
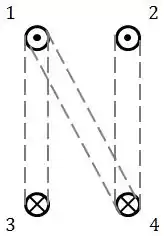
Os campos magnéticos gerados entre os elementos de fios superiores e entre os elementos de fios inferiores serão (a partir daqui, retiramos as linhas tracejadas para visualizarmos melhor nossas indicações vetoriais de campo e força ![]() ):
):
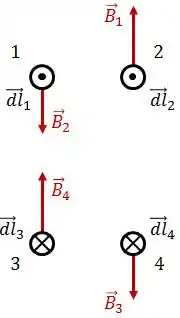
A força magnética sobre um fio condutor é dada por:
Logo, se considerarmos apenas uma pedaço infinitesimal do fio, teremos:
Como temos o produto vetorial entre e podemos utilizar a regra da mão direita para determinar o sentido das forças de interação entre esses elementos do fio.
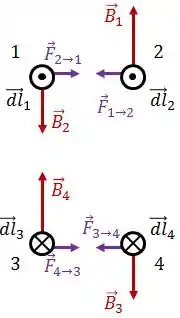
Assim, a força de interação entre esses elementos será uma força de atração. O mesmo acontecerá para todo o fio e as espiras se aproximam, como se a mola fosse comprimida.
A afirmação é verdadeira.
De uma forma bem mais simplificada, como em um verdadeiro ou falso não é necessário justificar, você pode manter em mente que entre correntes paralelas a força entre elas é de atração, já entre correntes anti paralelas a força entre elas é de repulsão.
Passo 4
Em um fio condutor ôhmico dado, ao dobrarmos a diferença de potencial entre suas extremidades, dobramos sua resistência.
A resistência de um fio é dada por:
Assim, a resistência é uma grandeza que depende somente do material do fio (devido à resistividade ) e da geometria do mesmo (devido ao comprimento e a área da seção transversal ).
A afirmação é Falsa.
Se dobrarmos a diferença de potencial, o que dobrará será a corrente elétrica no fio.
Passo 5
O fluxo do campo magnético da Terra através da superfície correspondente ao território brasileiro é igual, em módulo, ao fluxo do campo magnético da Terra através da superfície correspondente a todo o resto do globo terrestre.
O campo magnético da Terra tem essa representação:
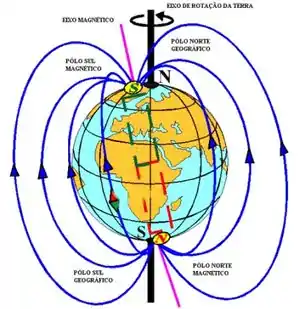
Assim, as linhas de campo magnético não chegam a atravessar a superfície do território brasileiro, bem como superfície correspondente a todo o resto do globo terrestre.
Portanto, o fluxo magn��tico através de qualquer parte de globo terrestre é nulo.
Dessa forma, fluxo magnético através do território brasileiro será o mesmo fluxo magnético através da superfície correspondente ao resto do globo terreste, que serão nulos.
A afirmação é verdadeira.
Passo 6
A lei de Ampère afirma que, para correntes estacionárias, o fluxo do campo magnético através de uma superfície é igual a vezes a corrente que atravessa .
A lei de Ampère não está associada ao fluxo magnético, e sim à circulação de campo magnético, dada por:
Logo, a afirmação é falsa.
Passo 7
Uma espira retangular de metal, originalmente sem corrente, está próxima de um fio longo e retilíneo, que transporta corrente, com dois de seus lados paralelos ao fio. O fio e a espira se encontram no mesmo plano. Quando a corrente do fio está diminuindo, a espira é atraída pelo fio.
A situação descrita é basicamente esta:
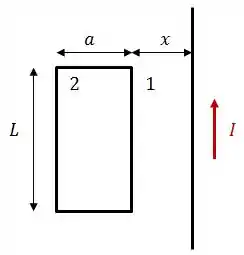
Onde chamamos 1 é o lado do retângulo paralelo ao fio e mais próximo do mesmo, 2 é o lado do retângulo paralelo ao fio e mais distante do mesmo, e são as dimensões da espira retangular, é a distância entre o retângulo e o fio, e é a corrente conduzida pelo fio.
A força magnética sobre um fio retilíneo é dada por:
Onde é a corrente que será induzida na espira.
O campo magnético gerado pelo fio a uma distância do mesmo é dado por:
Para os fios e , teremos:
Como o campo magnético é mais forte no fio 1, o sentido da força resultante sobre o retângulo será o mesmo da força sobre o fio 1. Agora nos resta saber o sentido da corrente induzida.
Utilizando a regra da mão direita, podemos ver que o campo magnético gerado pelo fio, no interior da espira estará apontando para fora do plano da página.
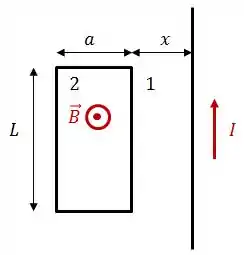
Como a corrente no fio está diminuindo com o tempo, o m��dulo do campo magnético também diminuirá e, por consequência, também o fluxo magnético.
Assim, de acordo com a Lei de Lenz, o campo magnético induzido na espira retangular vai tentar “ajudar” este campo magnético, estando na mesma direção e sentido que o mesmo.
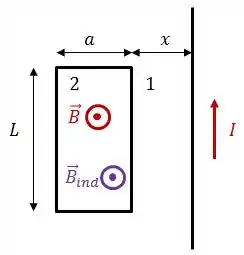
Dessa forma, utilizando a regra da mão direita, onde o polegar aponta no mesmo sentido de , concluímos que a corrente induzida estará no sentido anti-horário.
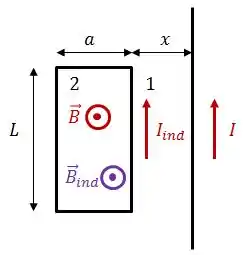
Como a corrente no fio 1 e a corrente no fio retilíneo são paralelas, a força entre elas será de atração, e a espira será atraída pelo fio.
Finalmente, a afirmação é verdadeira.
Passo 8
Para um condutor usual, como o cobre, o aumento da temperatura aumenta as vibrações moleculares, provocando maior espalhamento dos elétrons, o que faz com que sua resistividade diminua.
A resistividade varia com a temperatura de acordo com a equação abaixo:
Assim, se a temperatura aumenta , a resistividade também aumenta.
A afirmação é falsa.
Passo 9
Se a circulação do campo magnético ao longo de um caminho fechado for nula, não haverá nenhuma partícula carregada em movimento atravessando uma superfície aberta delimitada pela curva que descreve esse caminho.
Quando falamos em circulação de campo magnético, estamos falando em Lei de Ampère, dada por:
Se a circulação é nula, isso significa que . No entanto isso não significa necessariamente que não há nenhuma partícula carregada em movimento (corrente elétrica) atravessando a superfície delimitada pela curva que descreve esse caminho.
Significa que o somatório das correntes através dessa superfície é nulo. Logo, podemos ter duas correntes iguais, mas em sentidos opostos passando por essa superfície.
Assim, a afirmação é falsa.
Passo 10
A força magnética sobre uma espira carregando uma corrente estacionária, localizada em uma região de campo magnético uniforme é sempre nula, independentemente do formato da espira.
Vamos pensar aqui em uma situação aleatória onde temos uma espira retangular, conduzindo corrente no sentido anti-horário em uma região com campo magnético apontando para fora do plano da página.
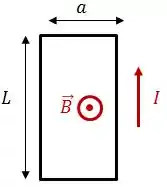
A força magnética sobre cada trecho retilíneo é dada por:
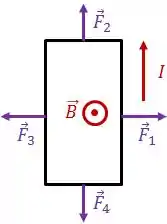
Como o módulo das forças e são iguais, bem como os módulos das forças e , a força resultando sobre essa espira será nula.
O mesmo ocorre para espiras de quaisquer formatos quando conduzem uma corrente estacionária em uma região com campo magnético uniforme.
A afirmação é verdadeira.
Resposta
V;
F;
V;
F;
V;
F;
V;
F;
F;
V;