Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Lei de Lenz

Ver Teoria
Exercício 49123456789101112131415161718192021222324252627282930313233343536373839404142434445464748505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394959697

Enunciado

Puc - Física 3 – P3 2018.2 - 1

Um trilho condutor em forma de semicircunferência de raio a = 10   c m está imerso numa região com campo magnético externo  B → de módulo B = 3,0   T (uniforme e constante), de direção perpendicular à página e com sentido saindo do papel. Um circuito elétrico de resistência total constante R = 0,5   Ω é completado por dois trilhos condutores retilíneos que partem do centro da circunferência: um horizontal, fixo, e outro móvel, que faz com o primeiro um ângulo variável θ t = 2,0 - 4,0   t + 4,0   t 2   [ r a d , s].

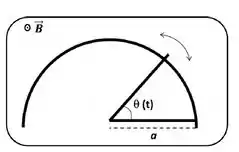
  1. Calcule a f e m induzida no circuito como função do tempo, ε i n d ( t ) . [Sugestão: Lembre que a área de um setor circular de raio a e ângulo θ em radianos é dada por A = π a 2 θ 2 π ] .
  2. Calcule o instante t N em que a corrente induzida se anula. Nos intervalos 0 < t < t N e t > t N , qual é o sentido da corrente no circuito, horário ou anti-horário? (Justifique.)
  3. Calcule o valor máximo i m a x que a corrente assume no intervalo 0 < t < 0,8   s .

    4. Considere ainda a mesma função θ ( t ) do enunciado principal, mas que agora o campo magnético externo B varie no tempo em vez de ser constante.

  4. Determine uma função B ( t ) para que a corrente induzida no circuito seja sempre nula.

Passo 1

a) Como o campo magnético  B → é perpendicular à página e está saindo dela, podemos colocar o vetor área  d A → também saindo da página e, portanto, paralelo à  B → .

Nesse caso, como  B → tem o mesmo valor em todos os pontos da superfície, ou seja, é uniforme, o fluxo do campo magnético é dado por

Φ B t = ∫ S B → ⋅ d A → = ∫ S B d A cos ⁡ 0 ° = B A t = B π a 2 θ t 2 π   .

Portanto, o fluxo magnético depende do tempo e é dado por

Φ B t = B a 2 θ t 2   .

Para encontrar a f e m induzida ε i n d , precisamos derivar o fluxo magnético em relação ao tempo. Como   B → e o raio a são constantes, ou seja, não variam com o tempo, ε i n d ( t ) tem a seguinte expressão

ε i n d t = - d Φ B t d t = - B a 2 2 d θ t d t = - B a 2 2 - 4 + 8 t   ,  

que, simplificada, vai resultar em

ε i n d t = B a 2 2 - 4 t   .

Substituindo os valores que o problema fornece, teremos

ε i n d t = 0,03 2 - 4 t V / m   .

Passo 2

b) A corrente induzida é dada por

i i n d t = ε i n d t R = 0,03 R   2 - 4 t   A / s   .

Portanto, i i n d t = 0 quando

2 - 4 t = 0     ⇒     t = 0,5   s   .  

Agora, a corrente induzida é positiva quando t < 0,5   s e negativa quando t > 0,5   s .

Como orientamos o vetor área paralelo a B → , então, pela regra da mão direita, o sentido positivo para a corrente será o anti-horário e o negativo, horário. Isso significa que, para t < 0,5   s , o sentido da corrente será anti-horário e, para t > 0,5   s , será horário.

Passo 3

c) Repare que a função que aparece em i i n d ( t ) é uma reta decrescente. Por isso, o maior valor que a corrente pode assumir acontece no instante t = 0 , momento em que a corrente será igual a

i i n d t = 0 = i m a x = 0,06 0,5       ⇒     i m a x = 0,12   A   .

Passo 4

d) Agora, temos um campo magnético que, para todo instante de tempo t , tem o mesmo valor em todos os pontos da superfície (uniforme) do circuito, mas que varia no tempo (não é mais constante) e está na mesma direção e sentido de antes. Portanto, continua valendo a seguinte expressão para o fluxo magnético

Φ B t = B t A t   .

Para que a corrente induzida seja nula

i i n d = - 1 R d Φ B t d t = 0     ⇒     d Φ B t d t = d d t B t A t = 0   .

Isso significa que a expressão que está entre parênteses deve ser uma constante, que chamaremos de Κ ≠ 0 . Disso, a gente tira que o campo magnético deve ser

B t = Κ A t = Κ a 2 1 - 2 t - 2 t 2   .

Resposta

  1. ε i n d t = 0,03 2 - 4 t V / m   ;
  2. i i n d = 0   → t = 0,5   s     ;     t < 0,5   s ,   a n t i - h o r á r i o   e   t > 0,5   s ,   h o r á r i o   ;
  3. i m a x = 0,12   A   ;
  4. B t = Κ A t = Κ a 2 1 - 2 t - 2 t 2   .

Exercícios de Livros Relacionados

20- Uma barra metálica com 1.50m de comprimento é puxada para a direita a 5.0m / s regulares e perpendicularmente a um campo magnético uniforme de 0.750T . A barra desliza sobre trilhos metálicos para
17- Use a lei de Lenz para determinar o sentido da corrente induzida que passa no resistor a b indicado na Figura 29.33 , quando ( a ) a chave S é aberta depois de ficar fechada durante alguns minutos
15- Um anel circular está em uma região do espaço onde existe um campo magnético uniforme, como indica a Figura 29.31 . O campo magnético está entrando no plano da figura. Determine o sentido (horário
18- Um tubo de papelão é circundado por dois enrolamentos feitos com dois fios isolados, formando espiras em sentidos contrários, como indica a Figura 29.34 . Os terminais a e b do enrolamento A podem
16- A corrente na Figura 29.32 obedece a equação I t = I 0 e - b t . Em que b0 . Determine o sentido (horário ou anti-horário) da corrente induzida na bobina redonda para t0 .