Na figura abaixo, o fio retilíneo longo transporta uma corrente e a espira retangular, de resistência , transporta uma corrente nos sentidos indicados. O fio e a espira encontram-se no mesmo plano.
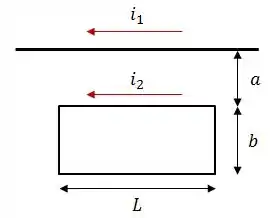
Calcule:
O vetor força magnética resultante que atua sobre a espira;
O fluxo do campo magnético produzido pela corrente através da área da espira;
Se a corrente crescer a uma taxa constante , determine o valor e o sentido
da corrente induzida na espira;
Passo 1
O vetor força magnética resultante que atua sobre a espira;
Beleza! A força magnética sobre um fio retilíneo é dada por:
Onde aponta na direção e sentido da corrente.
O campo magnético gerado pela corrente na espira terá o sentido saindo da página. Assim, o sentido da força magnética sobre cada parte da espira será o seguinte:
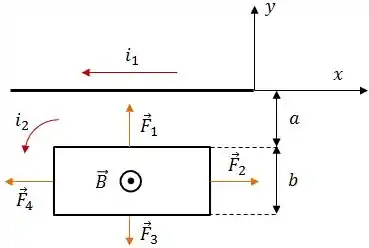
Pela geometria do problema, não é difícil ver que . Logo, as forças horizontais vão se cancelar. Isso significa que temos apenas que nos preocupar com as verticais.
Assim, vamos calcular somente e.
Passo 2
O campo magnético no fio 1 é dado por:
Assim, a força no fio 1 será:
O campo magnético no fio 3 é dado por:
Assim, a força no fio 1 será:
Portanto, a força resultante na espira será:
Passo 3
O fluxo do campo magnético produzido pela corrente através da área da espira;
Por definição, o fluxo magnético é dado por:
Aqui, o campo magnético gerado pela corrente é:
Além disso, podemos dizer que . Onde .
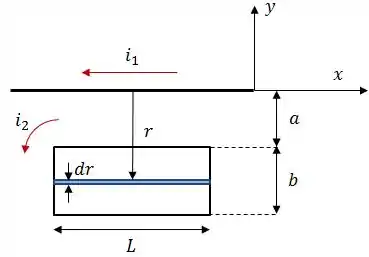
Agora só temos que voltar para a integral:
Passo 4
Se a corrente crescer a uma taxa constante , determine o valor e o sentido
da corrente induzida na espira;
Se está havendo uma variação na corrente , haverá uma variação no fluxo magnético na espira que, por sua vez, vai gerar uma induzida.
Para calcularmos a corrente induzida, então, vamos calcular a induzida e depois encontrar a corrente induzida através da Lei de Ohm:
Pela Lei de Faraday:
Como estamos interessados somente nos valores, não precisamos nos preocupar com esse sinal negativo.
Assim, a corrente induzida será dada por:
Pra fechar, precisamos descobrir o sentido dessa corrente.
Passo 5
De acordo com a Lei de Lenz:
O sentido de qualquer efeito de indução magnética é tal que ele se opõe à causa que produz esse efeito.
Simplificando... a corrente induzida é sempre do contra, se o fluxo magnético através da espira estiver aumentando, a corrente induzida vai gerar um campo magnético no sentido contrário, só pra atrapalhar... se o fluxo magnético estiver diminuindo, a corrente induzida vai gerar um campo magnético a favor.
Já que a corrente está aumentando, o fluxo magnético através da espira também está aumentando.
Assim, a corrente induzida vai gerar um campo que se oponha a esse aumento. Como o campo magnético na espira tem sentido saindo da página... o campo magnético induzido vai ter sentido entrando na página.
Pela regra da mão direita, para que o campo magnético gerado pela corrente induzida esteja entrando na página, a corrente induzida deve estar no sentido horário.
Resposta
A corrente induzida deve estar no sentido horário.