Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Lei de Lenz

Ver Teoria
Exercício 94123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293959697

Enunciado

Um fio muito longo (que podemos considerar infinito) e paralelo ao eixo x está transportando uma corrente variável no tempo I t > 0 . Uma espira quadrada de lados a e b e resistência total R está se deslocando no sentido positivo do eixo y com uma velocidade constante V . A distância entre o fio e o primeiro segmento da espira é r ( t ) (que também varia no tempo). O sistema está ilustrado na figura abaixo

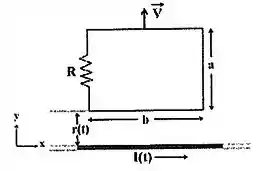
  1. Encontre a expressão para o fluxo do campo magnético Φ B t associado à espira.
  2. Encontre a expressão para da f e m induzida na espira em função da distância r t e da velocidade V .

    3. Suponha agora que a espira para uma distância de 1 m do fio ( r = 1 m ). Neste instante a corrente no fio está aumentando com uma taxa de 0,1 A / s .

  3. Qual é o sentido da corrente induzida na espira?

Passo 1

Temos que o fio com corrente I ( t ) produzirá um campo magnético sobre a espira. Esse campo pela regra da mão direita (e como a corrente se desloca no sentido positivo do eixo x ) na região da espira estará apontando na direção saindo da página.

Segundo a lei de Ampére temos que

∮ B → . d → = μ 0 I t

No plano x y

2 π y B = μ 0 I t

B → = μ 0 I t 2 π y z ^

Passo 2

Agora iremos calcular o fluxo desse campo magnético na espira. Como ela é retangular e está contida no plano x y , o seu vetor de elemento de área é dado por

d A → = d x d y z ^

(A escolha de d A → na direção positiva de z significa que supomos o sentido da corrente anti-horário para um fluxo positivo)

Assim o fluxo do campo magnético é dado por

Φ B t = ∫ d A → . B → = ∫ 0 b d x ∫ r t r t + a d y μ 0 I t 2 π y

Φ B ( t ) = μ 0 b 2 π I t ln ⁡ r t + a r t

Onde a dependência com o tempo está nos termos I ( t ) e r ( t ) .

Passo 3

A lei de Faraday diz que

ε = - d Φ B t d t = - μ 0 b 2 π d d t I t ln ⁡ r t + a r t

Usando a regra do produto na derivada

ε = - μ 0 b 2 π d I t d t ln ⁡ r t + a r t + I t d d t ln ⁡ r t + a r t

A última deriva é meio grandinha, então vamos faze-la separada e lembrando de usar a regra da cadeia!

d d t ln ⁡ r t + a r t = d d t ln ⁡ r t + a - ln ⁡ r = 1 r t + a - 1 r t d r t d t

Agora basta lembrar que a derivada temporal da posição r ( t ) é a velocidade V (que é constante, segundo o enunciado)

d d t ln ⁡ r t + a r t = 1 r t + a - 1 r t V

Assim

ε = - μ 0 b 2 π d I t d t ln ⁡ r t + a r t + I t 1 r t + a - 1 r t V

Ficou esse bichão grandão aí! o/

Passo 4

Como a espira está parada e a corrente no fio infinito está aumentando, temos que o fluxo magnético está aumentando.

Como o campo na espira está apontando para fora da página, temos que a corrente induzida na espira irá produzir um campo na direção contrária ao campo da corrente do fio infinito (de modo a tentar impedir a variação de campo magnético em seu interior), ou seja na direção para dentro da página

Para produzir tal campo, é necessário que na espira haja uma corrente induzida no sentido horário segundo a regra da mão direita

Resposta

(a) Φ B t = μ 0 b 2 π I t ln ⁡ r t + a r t

(b) ε = - μ 0 b 2 π d I t d t ln ⁡ r t + a r t + I t 1 r t + a - 1 r t V

(c) Horário

Exercícios de Livros Relacionados

20- Uma barra metálica com 1.50m de comprimento é puxada para a direita a 5.0m / s regulares e perpendicularmente a um campo magnético uniforme de 0.750T . A barra desliza sobre trilhos metálicos para
17- Use a lei de Lenz para determinar o sentido da corrente induzida que passa no resistor a b indicado na Figura 29.33 , quando ( a ) a chave S é aberta depois de ficar fechada durante alguns minutos
15- Um anel circular está em uma região do espaço onde existe um campo magnético uniforme, como indica a Figura 29.31 . O campo magnético está entrando no plano da figura. Determine o sentido (horário
18- Um tubo de papelão é circundado por dois enrolamentos feitos com dois fios isolados, formando espiras em sentidos contrários, como indica a Figura 29.34 . Os terminais a e b do enrolamento A podem
16- A corrente na Figura 29.32 obedece a equação I t = I 0 e - b t . Em que b0 . Determine o sentido (horário ou anti-horário) da corrente induzida na bobina redonda para t0 .