Faz-se girar uma bobina retangular, contando espiras de comprimento e largura , com uma frequência na presença de um campo magnético uniforme , como mostra a figura abaixo.
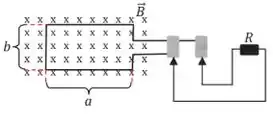
(a) Mostre que a f.e.m. induzida que aparece na bobina é dada por:
(b) Projete uma bobina para a qual seja igual a , quando girada revoluções por segundo, na presença de um campo magnético de
Passo 1
(a) Mostre que a f.e.m. induzida que aparece na bobina é dada por:
O fluxo do campo magnético é dado por:
em que
Já a f.e.m. é dada por:
onde é o número de espiras.
Assim sendo, utilizando as equações acima, chegamos em:
Passo 2
(b) Projete uma bobina para a qual seja igual a , quando girada revoluções por segundo, na presença de um campo magnético de
Para os valores do enunciado, temos que:
Resposta
(b)