Um solenóide real, de comprimento e seção transversal circular de raio , é colocado próximo a uma espira condutora de raio e espessura muito menor que . O plano da espira é posicionado paralelamente ao plano de uma seção transversal do solenóide, e ambos possuem o mesmo eixo de simetria , conforme mostrado na figura abaixo.
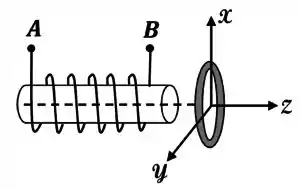
Considere as seguintes situações:
- Uma corrente quase-estacionária, que aumenta proporcionalmente com o tempo, circula no solenóide de para .
- Uma corrente quase-estacionária, que aumenta proporcionalmente com o tempo, circula no solenóide de para .
O que acontecerá com a espira condutora nas duas situações acima?
- Em ambas as situações, será repelida pelo solenóide.
- Em será atraída e em será repelida pelo solenóide
- Em ambas as situações, será atraída pelo solenóide.
- Em será repelida e em será atraída pelo solenóide.
- Não será atraída nem repelida em nenhuma das situações.
Passo 1
Para matar essa questão, galera, faremos a análise dos itens e separadamente. Esse problema é interessante porque tem bastante assunto fundamental envolvido e importante e que recorrentemente cai nas provas.
Para começar, então, representamos, na figura abaixo, a característica mencionada no item : uma corrente que aumenta com o tempo no sentido de para . Nesse caso, pela regra da mão direita, a gente vê que o campo que atravessa a espira tem o mesmo sentido do elemento de dessa espira, ou seja, apontando para .
Como e têm o mesmo sentido (), concluímos que o fluxo magnético é positivo neste caso:
Como o campo magnético está aumentando com o tempo e no mesmo sentido da área da espira, a taxa desse aumento é positiva, ou seja,
em que é a fem induzida na espira.
Pela regra da mão direita, o sentido positivo é aquele mostrado na figura com a seta em vermelho: se você olha a espira no sentido , o sentido positivo é o anti-horário.
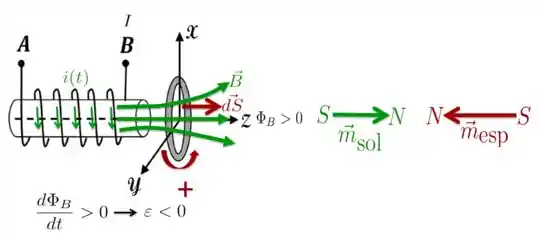
Como , a corrente induzida que aparece na espira tem sentido negativo. Então, se você olha a espira na direção , você vai ver a corrente no sentido horário.
Passo 2
Tanto para a corrente no solenóide, quanto para corrente induzida na espira, podemos associar um momento de dipolo magnético. A direção desse dipolo será aquele do campo magnético associado.
Por exemplo, para a corrente do solenóide acima, o momento de dipolo associado ao solenóide apontará no sentido de e podemos considerá-lo como se fosse um ímã cujo sentido sul-norte aponta também em , como na figura acima.
No caso da corrente induzida na espira, o ímã associado teria sentido sul-norte apontando para e seu momento de dipolo é . Por isso, neste caso, como pólos mesmo sinal se repelem, a espira será repelida pelo solenóide.
Passo 3
O item é exatamente o oposto do item . A corrente também aumenta, mas de para. Por essa razão, como mostra a figura abaixo, o campo produzido por ela também muda de sentido e agora está em sentido contrário ao do elemento de área .
Nessa situação, então, temos
e a corrente está no sentido positivo da figura, isto é, é vista no sentido anti-horário se olhada, à direita da espira, na direção .
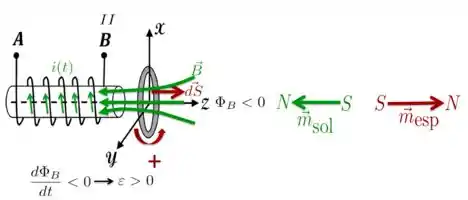
Agora, diferente do caso anterior, o sentido sul-norte dos dipolos apontam no sentido oposto. CONTUDO, PORÉM, TODAVIA, POLOS DE MESMO NOME AINDA CONTINUAM PRÓXIMOS!!
Por isso, também neste caso do item , a espira é repelida pelo solenóide !!
Concluímos, então, que em ambas as situações, a espira condutora será repelida pelo solenóide.
Resposta
Portanto, a letra a) é a resposta correta.