Uma esfera de massa 400 g e raio 4 cm é liberada, a partir do repouso, do topo de uma rampa inclinada de 25º com relação à horizontal. A rampa tem comprimento de 2.1 m. A esfera rola sem deslizar até o fim da rampa.
a) Qual é a velocidade angular da esfera no final da rampa?
b) Qual fração da energia cinética da esfera é rotacional?
Passo 1
Quando a gente tinha corpos descendo em planos inclinados, para encontrar a velocidade deles, a gente fazia a conservação da energia mecânica, lembra?
Aqui a ideia vai ser a mesma, só que na nossa energia mecânica, vamos ter também a energia cinética de rotação.
Então, vamos dar uma olhada no movimento e colocar o nosso nível de referência para a energia potencial gravitacional.
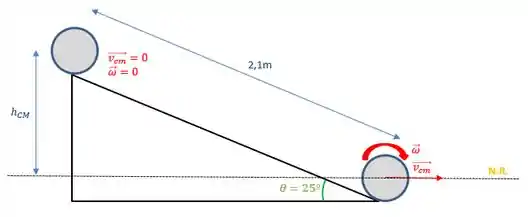
Passo 2
Realizando a conservação da energia mecânica teremos:
Pela tabela, sabemos que o momento de inércia de uma esfera rotacionando ao redor do centro de massa é
Com isso teremos:
Passo 3
Em um rolamento sem deslizamento, nós temos a seguinte relação entre a velocidade do centro de massa e a velocidade de rotação:
Substituindo, teremos:
Pelo desenho do movimento, percebemos que podemos encontrar a altura .
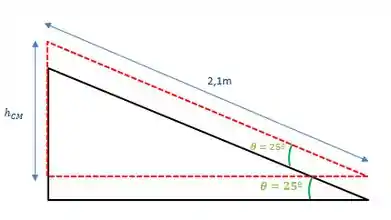
Avaliando o triângulo tracejado em vermelho:
Agora é só substituir os valores!
Passo 4
Agora falta responder a letra b).
Podemos encontrar a energia cinética total.
Realizando as substituições, teremos:
Sendo que a energia cinética de rotação é dada por:
Portanto, a fraça de energia cinética que é energia cinética rotacional é dada por:
Resposta
a)
b)