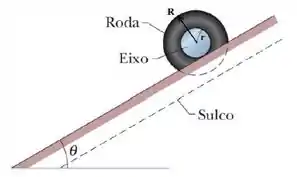
Uma roda homogênea é constituída por um disco maciço, uniforme, de massa , com um orifício de raio externo e raio interno . Há um eixo encaixado nele rigidamente (veja a figura).
O eixo que passa pelo orifício é cilíndrico, maciço, homogêneo, tem raio e a mesma massa . O momento de inércia do conjunto roda-eixo em relação ao centro de massa do eixo é . A roda está inicialmente em repouso no alto de uma rampa que faz um ângulo , pequeno, com a horizontal. Essa rampa possui um sulco aberto e largo no qual a roda se encaixa, sem tocá-la. O eixo está apoiado na rampa.
Após ser liberada, a roda rola suavemente, sem deslizamento, para baixo com seu centro de massa descendo uma distância .
- Determine uma expressão literal para o valor da velocidade angular da roda no final da distância , em função dos dados citados. Sugestão: faça por energia.
- Determine uma expressão literal para o valor da força de atrito estático sobre da roda durante a descida em função dos dados citados.
Passo 1
Primeiro detalhezinho aqui é ver que a massa que vamos usar é a massa total do sistema (roda + eixo), ou seja, .
Depois da roda ter deslocado uma distância na rampa, houve uma variação de altura dada por
E a variação de energia potencial gravitacional seria dada por
Já a variação de energia cinética é dada por
Onde , pois a roda é solta do repouso.
Por conservação de energia temos que
Passo 2
Como temos um rolamento sem deslizamento, temos
Assim
Isolando a frequência
Passo 3
Primeiramente vamos apontar todas as forças!
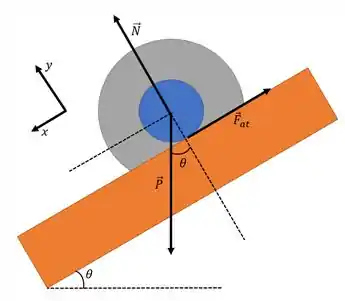
Bem, normalmente calcularíamos a força de atrito usando
Só que não temos o coeficiente de atrito ! Então vamos ter que achar a força de atrito por outro meio.
E como vamos fazer isso? A dinâmica da nossa roda é alterada pela força de atrito.
A segunda lei de Newton para translação ao longo da rampa fica
Então para achar a força de atrito basta achar a aceleração!
Passo 4
Agora vamos escrever a segunda lei para rotações. Como a força peso e a normal não exercem torque (pois apontam na direção do centro de massa), temos
Como a roda rola sem deslizamento podemos relacionar a aceleração linear com a aceleração angular por
Assim
E podemos substituir essa aceleração na segunda lei de Newton
Passo 5
E tadááá! Aí a nossa resposta ;)
Resposta
(A)
(B)