Determine a derivada direcional da em , sendo um versos dado pelo ângulo .
Então a derivada direcional da no ponto será:
Passo 1
Lembra como se calcula uma derivada direcional?
Se temos uma função , e queremos a deriva dela na direção do vetor , temos que fazer o seguinte:
Ou seja, temos que fazer o produto interno entre o gradiente da função e o vetor .
O produto interno é uma operação entre dois vetores, que resulta em um número, e segue essa fórmula aqui:
E a fórmula do vetor gradiente de uma função, é essa:
Passo 2
Ok, nosso primeiro passo é calcular esse gradiente. Para isso, precisamos achar as duas derivadas parciais:
E agora em relação a :
Então, o vetor gradiente é:
Passo 3
Agora precisamos achar . O enunciado disse que é um versor (isso quer dizer que é um vetor de módulo igual a ) dado pelo ângulo .
Isso quer dizer o seguinte:
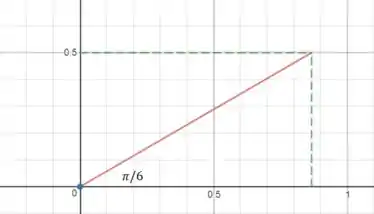
Então quais são as componentes do nosso versor? Já que ele tem comprimento , é só projetarmos ele nos eixos e :
Passo 4
Agora vamos voltar à fórmula da derivada direcional:
Seguindo aquela fórmula do produto interno:
Mas queremos calcular isso no ponto :
Sabemos que e :
Resposta
Letra (a).