Um avião monomotor, à altitude de , deixa cair uma caixa. No instante em que a caixa é largada, o avião voava a inclinado de acima da horizontal. Despreze a resistência do ar.
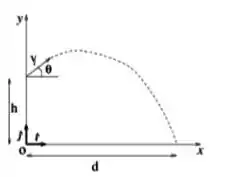
- A caixa atinge o solo a que distância horizontal do ponto em que é largada;
- Qual é o vetor velocidade da caixa ao se chocar com o solo.
Passo 1
No instante que a caixa atinge o solo, . Para o eixo :
Passo 2
Sabendo o tempo, basta calcular o alcance total. Para o eixo .
Passo 3
Para calcular a velocidade no instante em que a caixa atinge o chão, basta calcularmos e . Para o eixo , cuja aceleração é nula, temos:
Para o eixo , cuja aceleração vale , temos:
Passo 4
Usando a forma vetorial, temos:
O seu módulo é:
Resposta
- ;