Uma bola de futebol é chutada a partir do chão com uma velocidade inicial de e um ângulo para cima de . No mesmo instante um jogador a de distância, na direção do chute, começa a correr para receber a bola. Qual deve ser sua velocidade média para que alcance a bola imediatamente antes que toque o gramado?
Passo 1
O problema quer saber qual deve ser a velocidade do jogador para que ele alcance a bola. Para determinarmos a velocidade do jogador precisamos saber o quanto ele vai correr, ou seja, o alcance da bola e quanto tempo ele vai correr que seria o tempo de voo da bola.
Como ainda não sabemos o alcance da bola o jogador pode estar dentro desse alcance e aí ele teria que correr no sentido da bola. Ou fora do alcance e aí sua velocidade apontara para o sentido oposto. Como não temos o tempo percorrido vamos inicialmente adotar a hipótese do jogador fora do alcance da bola, só pra gente fazer um desenho.
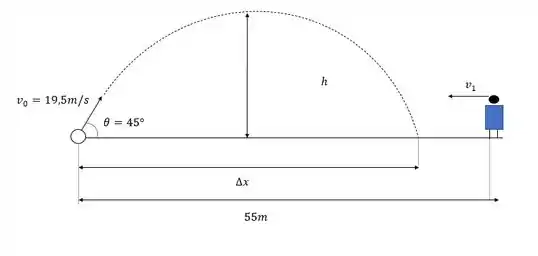
A partir daí vamos calcular o tempo de voo da bola e com isso o alcance, pra enfim definirmos a velocidade do jogador.
Passo 2
Pra calcularmos o tempo de voo vamos analisar apenas o movimento vertical da bola, pra isso a gente precisa decompor a velocidade na componente vertical.
Agora a gente pode usar a equação da velocidade, vamos analisar a subida da bola e para ela a equação fica:
Quando a bola sobe ela vai perdendo velocidade por causa da gravidade e atinge no ponto máximo, sendo assim:
Substituindo e , temos o tempo:
E não podemos esquecer que o tempo de subida é só metade do tempo do movimento, temos que usar o tempo total que é o dobro desse aqui pra analisar o alcance.
Passo 3
Vamos agora calcular o alcance da bola, no eixo não temos aceleração e por isso o alcance é dado por:
E lembrando que a velocidade em é:
Então o alcance fica:
Então o nosso desenho estava certinho, o jogador está a 55 metros da bola e precisa correr na direção oposta.
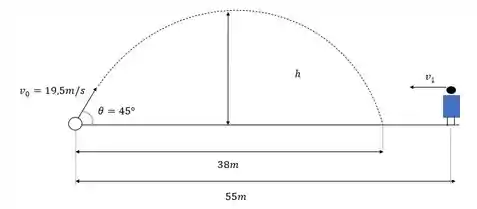
Passo 4
Agora que temos tudo basta substituir na equação da posição do movimento uniforme para descobrirmos a velocidade do jogador
A velocidade negativa significa que o jogador correrá no sentido oposto do movimento da bola e portanto a hipótese que adotamos estava correta pro movimento.