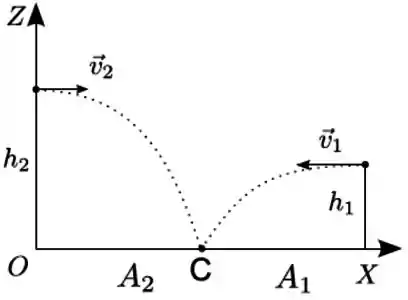
Dois projéteis 1 e 2 são lançados simultaneamente e horizontalmente de alturas e (diferentes) em relação ao solo. Verifica-se que ambos atingem o mesmo ponto no solo e têm o mesmo alcance . A razão entre os módulos e das velocidades de lançamento dos respectivos projéteis 1 e 2 é

(a)

(b)

(c)

(d)

(e)

Começando pelo movimento do projétil 2 no eixo vertical (eixo ). Ele sai de uma altura , com velocidade vertical nula, e sob a aceleração da gravidade .

Então as equações do seu movimento no eixo vertical são:

Já no eixo , o projétil sai da posição com velocidade inicial de módulo (apontando pra direita), e não tem aceleração, então suas equações horárias são:

Beleza, agora vamos dar uma olhada no projétil 1.

Seu movimento no eixo é quase o mesmo que pro projétil 2, a única diferença é que ele sai de uma altura :

Já no eixo , a coisa fica um pouco mais delicada, porque não sabemos qual é a posição inicial do projétil. Então vamos fazer o seguinte: vamos dizer que ele é lançado de cima do eixo e pra direita, que nem o projétil 2. Não vai fazer diferença porque o alcance dele vai ser o mesmo e ele vai cair no mesmo lugar, beleza?

E ele é lançado com velocidade de módulo , então temos:

Digamos que o projétil 2 chega no chão no tempo . Então, em , sua coordenada é nula!

Ou seja,

E quando o projétil chega no chão, sua coordenada é igual ao seu alcance . Portanto, no tempo , temos

Show! Agora vamos fazer a mesma coisa pro projétil 1, pra achar uma expressão de .

Chamando de o instante em que ele encosta no chão, temos:

As contas são idênticas às que fizemos antes, só trocando e por e !

Então isso vai dar:

Da mesma forma, quando o projétil 1 chega no chão, sua coordenada vale , então:

Portanto, obtivemos:

Então a razão é:

Dá pra cortar em cima e em baixo aí sobra:

Deu um trabalhão mas foi!