Um canhão lança suas balas com uma certa inclinação em relação à horizontal. Assuma que a bala atinge o chão na mesma elevação em que foi lançada.
Se o tempo de voo foi de segundos, qual a componente vertical de sua velocidade inicial?
(Considere )
50
nenhuma das anteriores
Passo 1
Pra começar bem a gente precisa entender a situação o canhão atira uma bala com uma inclinação em relação a horizontal e velocidade . O enunciado diz pra gente considerar que a bala chega no chão na mesma altura que foi lançada, é como se desprezássemos a altura do canhão.
Vamos então desenhar um esquema pra ver o que tá rolando ali.
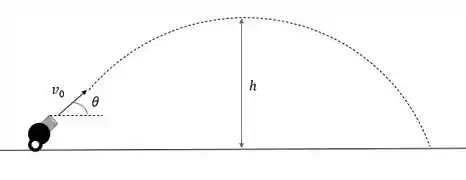
O problema quer que a gente encontre a componente vertical daquela velocidade , e nos dá o tempo de voo. Esse tempo de voo é simplesmente o tempo marcado pro percurso da bala sair do canhão e chegar no chão de novo.
O que vamos fazer aqui é trabalhar pensando só no movimento vertical da bala, olhando só a componente da velocidade.
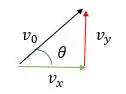
Como nos foi dado o tempo de voo, podemos considerar que a bala demora o mesmo tempo pra subir e pra descer, sendo assim até atingir a altura , o tempo é.
Passo 2
E agora é só a gente aplicar a equação da velocidade para o eixo vertical pensando na subida, olhando apenas pra velocidade .
Onde pro movimento de subida.
E o que vai acontecer quando a bala atingir a altura máxima? A velocidade dela será 0, e aí a relação vai ter essa cara.
Considerando que temos:
Resposta
Alternativa .