[ENUNCIADO COMUM ÀS QUESTÕES 1, 2 e 3 do 2°EE 2017.2]
Um esquiador de massa parte do repouso do ponto A, a uma altura acima da extremidade de uma rampa para saltos de esqui. Ele deixa a rampa no ponto B, fazendo um ângulo com a horizontal. O esquiador então atinge sua altura máxima no ponto C. Despreze os efeitos da resistência do ar e do atrito com a rampa. Dados: ; e .
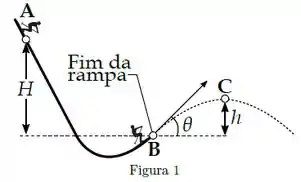
[Questão 2]
Achamos
[Questão 3 - ANULADA]
A altura máxima atingida pelo esquiador é:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Passo 1
Como conhecemos o módulo da velocidade em B e os valores de e , caímos em um problema bem comum de lançamento oblíquo, onde sabemos a velocidade de lançamento e sua direção.
Lembra que podemos analisar separadamente o movimento na vertical e o movimento na horizontal dentro de um lançamento oblíquo?
Então, como queremos a altura máxima da trajetória, só precisamos analisar o movimento na vertical.
Passo 2
O movimento na vertical está sujeito à aceleração da gravidade , logo podemos usar as equações de movimento uniformemente variado:
Como temos a velocidade, a aceleração e queremos achar uma distância, vamos usar Torricelli:
Passo 3
Mas quem é essa velocidade inicial ?
É a componente vertical de .
Então vamos decompor :
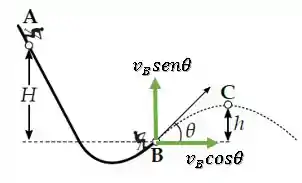
A componente da velocidade vertical é:
Passo 4
Agora vamos voltar à nossa equação do movimento:
Achamos a velocidade inicial , a velocidade final será nula no ponto máximo. Além disso, temos que a aceleração vale e o deslocamento será , que queremos encontrar.
OBS: A aceleração aponta no sentido contrário da velocidade inicial, por isso o sinal de negativo.
Pronto, achamos a altura , entretanto, a prova teve um erro e não existia a resposta correta dentro das alternativas. Essa questão foi anulada.
Resposta
QUESTÂO ANULADA: