Escrever a Tag aqui (nome do capítulo IGUALZINHO), Outra tag, Mais uma tag
Um projétil é lançado a partir do solo com vetor velocidade inicial de módulo 10 m/s, fazendo um ângulo com o eixo x horizontal. Sabe-se que cos = 0,80 e sen = 0,60. Considere . Despreze a resistência do ar.
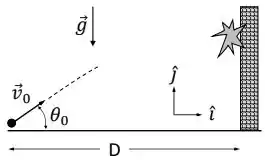
Após percorrer uma distância horizontal D = 8,0 m, o projétil se choca com um muro. Imediatamente antes deste choque, o vetor velocidade do projétil é, em m/s:
a)
b
c)
d)
e)
f)
g)
h)
i)
Passo 1
Primeiro vamos lembrar daquela decomposição de vetores:
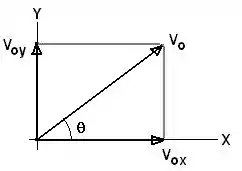
Onde:
E como sabemos, num movimento oblíquo, na horizontal temos um Movimento Uniforme, e na vertical um Movimento Uniforme Variado devido a apresença da aceleração da gravidade.
Então bora lá. Analisar cada movimento separadamente:
No eixo x, temos:
Então já temos a componente x do nosso vetor da resposta, porque a velocidae em x não muda, lembra? Showww!
Passo 2
Pô, e para o eixo y? Bom, podemos usar o eixo x pra descobrir o tempo em que o corpo chegou até aquele lugar e usar o tempo pra descobrir a velocidade em y! Show, então, em x temos um Movimento Uniforme, ou seja:
Pronto, agora podemos aplicar na fórmula da velocidade do movimento variado (no eixo y):
Pronto, terminamosss!
Resposta
f)