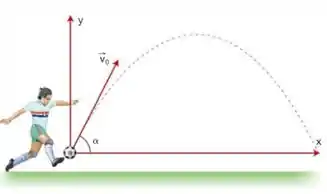
Suponha que em uma partida de futebol, o goleiro, ao bater o tiro de meta, chuta a bola, imprimindo-lhe uma velocidade cujo vetor forma, com a horizontal, um ângulo. Desprezando a resistência do ar, são feitas as seguintes afirmações.
I – No ponto mais alto da trajetória, a velocidade vetorial da bola é nula.
II – A velocidade inicial pode ser decomposta segundo as direções horizontal e vertical.
III – Se a bola alcançará a maior distância horizontal possível.
IV – No ponto mais alto da trajetória o valor da componente vertical da velocidade é nulo.
Estão corretas:
A) I, II e III
B) II, III e IV
C) II e IV
D) III e IV
E) I e II
Passo 1
Primeiro, vamos lembrar umas coisas importantes de um lançamento obliquo:
Temos aceleração da gravidade, que está na direção vertical. Logo, no eixo y temos um MUV.
Como não temos aceleração na direção horizontal, temos que no eixo x o movimento é uniforme MU.
O que temos que fazer é analisar o movimento em cada eixo separadamente. Beleza?
Então amos ver cada uma das alternativas
Passo 2
I – No ponto mais alto da trajetória, a velocidade vetorial da bola é nula.
O que acontece quando a velocidade de um corpo é zero? O corpo para!!
Quando a bola está na posição mais alta ela para? Não né!
Então essa tá errada.
Mas vamos analisar melhor. Lembra que temos que analisar os movimentos nas duas direções. Então, olha pra direção vertical, no ponto mais alto, a bola não consegue mais subir, então ela para, momentaneamente, e começa a cair.
Já na direção horizontal a bola tem velocidade constante, até ela atingir o alcance máximo.
Então na posição mais alta, apenas a componente da velocidade é zero.
Passo 3
II – A velocidade inicial pode ser decomposta segundo as direções horizontal e vertical.
Certíssimo! Podemos decompor qualquer vetor usando um eixo ortogonal e o ângulo que o vetor faz com um dos eixos.
É só usar a regra do COlado/SEparado; por exemplo nesse caso teríamos:
, pois o está COlado com o ângulo, e
, pois o está SEparado do ângulo.
não muda, pois temos um MU.
Essa velocidade em é a velocidade inicial, depois ela muda, já que temos aceleração na direção , ok?
Passo 4
III – Se a bola alcançará a maior distância horizontal possível.
Vamos olhar para o movimento horizontal. Como não temos aceleração, temos um MU.
O movimento começa na origem, então:. E como vimos antes, .
Então
Falta a gente descobrir qual é o tempo necessário para a bola chegar a seu alcance máximo.
Pensa aqui comigo... O tempo que a bola leva para subir tem que ser o mesmo tempo que a bola leva pra descer. Vamos olhar agora para o movimento na vertical:
Vimos que e . Vimos também que no ponto mais alto a .
Substituindo
Então o tempo de subida (ou descida é)
Assim, o tempo total, da subida e da descida é
Esse é o tempo correspondente ao tempo da viagem total, ou seja, é o tempo que a bola leva pra chegar no alcance máximo. Entao
Arrumando
Lembrando daquela relação trigonométrica
Então
Para o alcance ser máximo, temos que o seno deve ser máximo, isso acontece quando o ângulo é , ou seja
Logo, essa alternativa tá certa!!
Passo 5
IV – No ponto mais alto da trajetória o valor da componente vertical da velocidade é nulo.
Já discutimos isso... vimos que, de fato, no ponto mais alto da trajetória, a componente vertical da velocidade é nula porque o movimento inverte o sentido. Certíssima.
Resposta
Alternativa b.