PARTIDA DE FUTEBOL
"A chuteira veste o pé descalço
O tapete da realeza é verde
Olhando para bola eu vejo o sol
Está rolando agora, é uma partida de futebol
O meio campo é lugar dos craques
Que vão levando o time todo pro ataque
O centroavante, o mais importante
Que emocionante, é uma partida de futebol"
Trecho da canção Partida de Futebol, interpretada pelo grupo Skank e composta por Nando Reis e Samuel Rosa.
Um centroavante chuta a bola em certa direção com velocidade inicial , A trajetória descrita é parabólica e o projétil toca o solo horizontal em . Desprezando a resistência do ar, podemos afirmar que a opção FALSA, é:
(a) O tempo que a bola leva para subir e descer é igual ao tempo dela atingir o seu alcance máximo.
(b) o chute atinge a velocidade zero no eixo y no ponto mais alto da trajetória.
(c) A aceleração vetorial no eixo x é constante.
(d) O movimento do eixo y possui a aceleração da gravidade.
(e) O movimento do eixo x é um MUV e do eixo y é MU
Passo 1
Fala aí!!!
Temos um problema de lançamento oblíquo! Vamos lembrar algumas coisinhas importantes desse tipo de movimento e depois a gente analisa cada alternativa.
Acompanha comigo.
Quando a gente joga uma bola, ela tem um movimento na vertical e na horizontal acoplados, certo? Além dela subir e descer ela vai pra frente.
O importante a se notar é: na direção vertical temos a aceleração da gravidade. Logo, nessa direção a velocidade varia. Como era de se esperar, né? Se a velocidade não variasse a bola iria ficar subindo eternamente. Chega um momento (no ponto mais alto da trajetória) que a velocidade vertical para (momentaneamente) e aí o sentido do movimento muda, a bolinha para de subir e começa a descer.
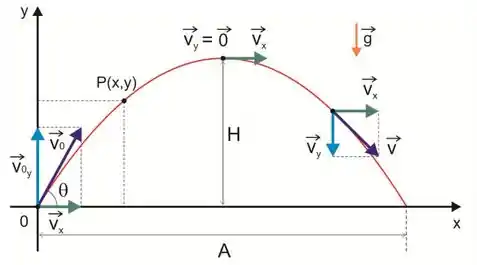
Já na direção x, não temos aceleração, então a velocidade é constante nessa direção, logo é um movimento uniforme.
Isso quer dizer que uma certa distância é percorrida no mesmo intervalo de tempo, pois a velocidade é costante. Por exemplo, a distância percorrida até a bolinha chegar na altura mais alta é . Vamos supor que o tempo que ela demora pra chegar lá é A velocidade horizontal é :
Se considerarmos o deslocamento do ponto mais alto até o ponto mais baixo, ou seja, a segunda metade do alcance, temos que: e a velocidade ainda continua a mesma, pois é constante:
Comparando as duas equações, vemos que:
Ou seja, o tempo de subida é igual ao tempo de descida!
Beleza até aqui?
Vamos analisar as alternativas.
Passo 2
(a) O tempo que a bola leva para subir e descer é igual ao tempo dela atingir o seu alcance máximo.
Sim!! Pois vimos que o tempo que a bola demora para chegar até a altura mais alta (metade do alcance) é igual ao tempo de descida. Então o tempo o tempo para ela chegar ao seu alcance máximo é a soma dos tempo que ela demora para subir com o tempo que ela demora para descer.
Essa tá certa!!
Passo 3
(b) o chute atinge a velocidade zero no eixo y no ponto mais alto da trajetória.
Certíssima! No ponto mais alto da trajetória, a bolinha para, momentaneamente, e troca o sentido de movimento, ela começa a cair, pois, como é o ponto mais alto, ela não consegue mais subir. Ela para e começa a cair.
Passo 4
(c) A aceleração vetorial no eixo x é constante.
Sim!! Em x não temos aceleração, então nesta direção o movimento é uniforme, então a aceleração é nula!!
Passo 5
(d) O movimento do eixo y possui a aceleração da gravidade.
Sim! A direção do vetor aceleração da gravidade está na vertical. Mesma direção do eixo y.
Passo 6
(e) O movimento do eixo x é um MUV e do eixo y é MU
MUV é o movimento uniformemente variado, ou seja, a velocidade varia, pois existe uma aceleração não nula. No eixo x, vimos que a aceleração é nula, e a bolinha descreve um movimento com velocidade constante, nesta direção, então em x, o movimento é uniforme.
Em y, temos a aceleração da gravidade. Que varia o módulo da velocidade vertical assim, o movimento em y é um MUV.
Essa alternativa tá errada!
Resposta
Alternativa (e)