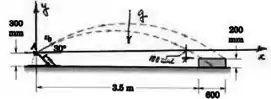
Uma equipe de estudantes de engenharia está projetando uma catapulta para lançar uma pequena bola em A de modo que ela caia na caixa. Sabendo que o vetor velocidade inicial faz um ângulo de com a horizontal.
- Obtenha a equação da trajetória
- Determine a faixa de velocidades de lançamento com a qual a bola cairá dentro da caixa
Passo 1
Letra a)
Pra começar vamos pensar em
Eixo x
Como não possui aceleração, no eixo x apenas temos que nos preocupar com a velocidade.
Eixo y
Agora pensando no eixo , temos que pensar na gravidade também.
Passo 2
Agora que já sabemos cada eixo em função do tempo, vamos substituir o tempo em uma das equações
Passo 3
Os pontos que fazem parte da caixa são
Sendo assim, vamos substituir na equação da trajetória e achar os valores possíveis que de
Resposta
Exercícios de Livros Relacionados
Suponha que o ângulo inicial α 0 da Figura 3.26 seja 42,0 ° e que d seja igual a 3,0 m. Onde o dardo e o macaco se encontrarão, se a velocidade inicial do dardo for a) 12,0 m/s? b) 8,0 m/s?c) O que oc
Galileu mostrou que, se os efeitos da resistência do ar são ignorados, os alcances de projéteis (no mesmo nível) cujos ângulos de projeção diferem de 45°, para mais e para menos, do mesmo valor, são i
Em 1939 ou 1940 , Emanuel Zacchini levou seu número de bala humana a novas alturas: disparado por um canhão, passou por cima de três rodas-gigante antes de cair em uma rede (Fig.4-39). (a) Tratando Za
Os esquiadores experientes costumam dar um pequeno salto antes de chegarem a uma encosta descendente. Considere um salto no qual a velocidade inicial é v 0 =10m / s , o ângulo é θ 0 =9,0 ° , a pista a
Cortina da morte. Um grande asteroide metálico colide com a Terra e abre uma cratera no material rochoso abaixo do solo, lançando pedras para o alto. A tabela a seguir mostra cinco pares de velocidade