Uma bola, de dimensões reduzidas, é lançada do nível do solo com uma certa velocidade inicial de módulo conhecido, atinge o solo novamente a uma certa distância do ponto de lançamento. Dependendo do ângulo de lançamento que o vetor velocidade inicial faz com a direção horizontal, essa distância varia. A figura abaixo dá o alcance da bola para uma mesma velocidade inicial quando variamos o ângulo de lançamento.
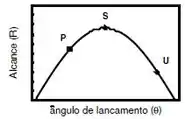
O módulo da velocidade ao alcançar a altura máxima, para cada um dos três ângulos de lançamento indicados na figura, obedece a relação:
(a)
(b)
(c)
(d)
(e)
(f)
Passo 1
Ao alcançar a altura máxima, apenas a componente x da velocidade atua sobre a bola. Esta velocidade vale:
Como o cosseno de um ângulo vale para o ângulo e diminui quando aumenta-se o ângulo, podemos dizer que quanto menor o ângulo de lançamento, maior a velocidade no ponto mais alto. Assim: