Você tem um estilingue que arremessa projéteis a uma velocidade de , e pretende atingir alguns alvos com esse estilingue. Assuma que .
(a) Qual a distância horizontal máxima que você pode atingir com o seu projétil, assumindo que você atira o projétil desde o solo, e que o alvo também está no solo, na mesma altura do estilingue?
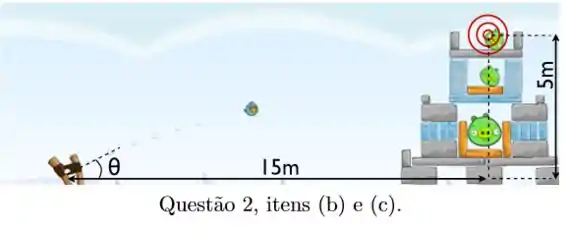
(b) Você quer arremessar o seu projétil (digamos, um “angry bird”) e atingir um alvo (digamos, um porquinho) que se encontra a uma distância de na horizontal, e a uma altura de na vertical, como indicado na Figura. Encontre a equação que determina o valor de a tangente do ângulo com o qual você deverá inclinar o seu estilingue. ( Dica: lembre-se que ).
(c) Agora, considere que entre o seu estilingue e o alvo existe um obstáculo que impede que você lance os projéteis com uma inclinação menor que 60°, ou seja, você só pode lançar projéteis com ângulos . Qual é o valor de que permite que você atinja o seu alvo?
Passo 1
(a)
As distâncias horizontal e vertical são dadas por:
Podemos unir as duas equações eliminando o parâmetro que não temos pelo enunciado. Fica assim:
Substituindo na segunda equação:
Fazendo a substituição que o enunciado deu como dica , temos:
Como o alvo está no solo, , então:
Temos então duas soluções, , que não é a solução que queremos né? E temos também
Queremos a distância máxima, podemos acha-la se a tangente for máxima, ou seja, quando , (), temos que a distância máxima é então:
Passo 2
(b)
Basta utilizar a equação que encontramos no item anterior, mas usando os dados: , , e , temos:
Passo 3
(c)
Utilizando a equação do item anterior, se chamarmos de , teremos:
Resolvendo essa equação do segundo grau, achamos duas soluções.
Ou seja, e . O ângulo da primeira solução é 45°, portanto menor que o ângulo mínimo especificado na questão. O ângulo correspondente à segunda solução é maior do que 60°, já que . Portanto, temos que .
Resposta
(a)
(b)
(c)