Darlene é uma motociclista de circo. Como clímax de seu show, ela larga de uma rampa inclinada de , salta um fosso de largura e pousa em um rampa mais elevada (altura ) do outro lado . Para uma dada altura , encontre a mínima rapidez de largada necessária para ela realizar o salto com sucesso. Quanto vale para , e ?
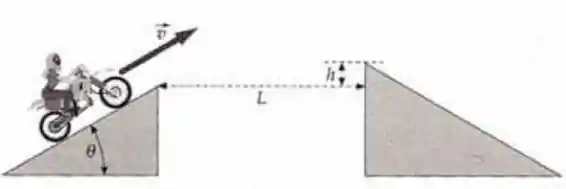
Mostre que, independente da rapidez de largada, a altura máxima da plataforma é . Interprete fisicamente este resultado. (Despreze a resistência do ar e trate a motoqueira e a moto como se fossem uma única partícula.)
Passo 1
O problema quer saber a velocidade mínima com que é possível realizar esse salto. Acharemos se acharmos a velocidade inicial a qual em um instante a moto tenha percorrido em e esteja na altura .
Pois se a moto tiver em uma altura menor que significa que ela não consegue fazer o salto e se altura for maior que ela não estava na velocidade mínima possível.
Passo 2
Vamos escrever a equação da posição no eixo
Lembrando que
Queremos o instante de tempo no qual a motociclista percorre a distância no eixo
Passo 3
Agora vamos estudar o movimento no eixo , escrevendo a equação da posição temos:
Como
Agora substituímos e
Como falamos no “passo 1” para achamos a velocidade mínima é preciso que o instante de tempo que a moto alcance a distância em ela esteja na posição em .
Como vimos que precisamos que isso ocorra no mesmo instante de tempo , basta substituirmos o valor de que achamos no “passo 2” para descobrirmos
Passo 4
Terminamos de achar uma equação para , então basta substituir os valores dados
Passo 5
Como raíz de um número negativo não existe no conjuto de números reais, se
Teriamos raíz de um número negativo o que não é possível. Se pensarmos no caso onde
teríamos uma divisão por zero e por isso a velocidade mínima iria tender ao infinito.
Então só é possível excutar esse salto se