João e Pedro estão no topo de um prédio. Eles jogam uma bola cada, ao mesmo tempo. João arremessa sua bola verticalmente para baixo. Pedro arremessa sua bola para frente e para baixo, fazendo um ângulo de com a horizontal. A rapidez inicial da bola de Pedro é o dobro da de João. Supondo que não haja desníveis no chão próximo ao prédio, qual das bolas atinge o solo primeiro?
(A) A bola de Pedro.
(B) A bola de João.
(C) Elas chegam ao solo ao mesmo tempo.
(D) A resposta depende da altura do prédio.
(E) A resposta depende do módulo das velocidades iniciais.
Passo 1
Vamos chamar a velocidade da bola arremessada por Pedro de e a velocidade da bola arremessada por João de .
Temos a seguinte relação:
O tempo de queda vai estar inteiramente ligado à componente da velocidade vertical.
Ou seja, basta comparar entre as duas bolas arremessadas, qual que vai ter a maior componente da velocidade na vertical.
Passo 2
A primeira bola, arremessada por João, foi jogada verticalmente para baixo:

Então, a componente vertical de sua velocidade é a própria velocidade inicial:
Passo 3
Já a bola arremessada por Pedro faz um ângulo de com a horizontal:
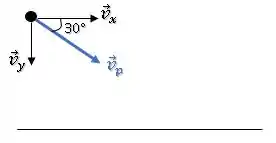
Então, a componente vertical de sua velocidade é:
Mas lembra lá no início que?
Substituindo isso na componente vertical da bola arremessada por Pedro:
Passo 4
Ou seja, se as duas componentes verticais de velocidade são iguais entre si:
Isso significa que os tempos de queda serão os mesmos, independente do movimento na horizontal. Então, ficamos com a letra (C).
Resposta
Letra (C)