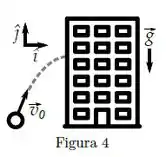
Uma partícula é lançada do solo no instante com velocidade (em ) (ver Figura 4). No instante , a partícula se choca com um edifício. Qual é a altura (em relação ao solo) do ponto de colisão? Use .

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

Se já sabemos o instante em que a partícula se choca e queremos descobrir a altura que ela bate no prédio, vamos analisar o movimento na vertical.

Bom, na vertical, a partícula realiza um movimento uniformemente variado, então podemos escrever sua posição em função do tempo com a seguinte expressão:

Já que estamos falando de altura, vamos escrever a posição como :

Além disso, temos que a aceleração será a da gravidade e ela aponta para baixo. Por isso vamos escrever com um sinal de negativo:

A partícula parte do solo, então sua altura inicial é zero . Já sua velocidade vertical inicial será a componente em da velocidade, assim, :

Então, ficamos com a expressão da altura em função do tempo como:

Por último, basta usar a expressão de para encontrar a altura no instante (momento da colisão):

Então, achamos que a resposta é a alternativa (d).