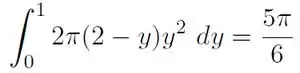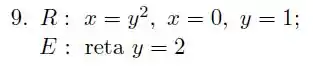
Passo 1
O lance é esboçar o mais precisamente possível os gráficos das funções pra entender bem a região :
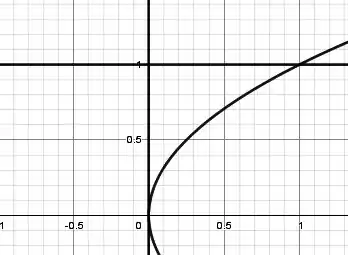
Passo 2
Então é a área entre as três curvas em preto, em que .
Assim, o volume do sólido todo é:
Perceba que fazemos porque fazemos o cara que está mais a esquerda menos o cara que está mais a direita.
Vamos resolver essa integral:
Resposta
Exercícios de Livros Relacionados
Nos Exercícios 23-26, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões delimitadas pelas curvas dadas em torno das retas dadas.26 - y = x 4ey = 4 - 3 x 2 B
Para algumas regiões, os dois métodos funcionam bem para sólidos obtidos com a rotação da região em torno dos eixos das coordenadas, mas isso nem sempre ocorre. Por exemplo, quando uma região gira em