UFCG – Sem Campus – Cálculo Diferencial e Integral II – Listas de Cálculo 2 – UAMat – Lista 3 – Questão 9d
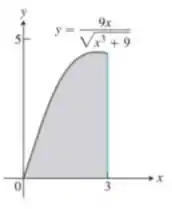
Use o método da casca para determinar os volumes dos sólidos obtidos com a rotação da região sombreada em torno do eixo :
Passo 1
Fala aí gente, tudo tranquilo?
Nesse exercício temos uma região no plano , como mostrada na figura abaixo:
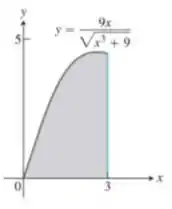
É a região que está abaixo da curva:
No intervalo:
Pegando essa região e rotacionando em torno do eixo , obtemos um sólido de revolução. O enunciado nos pede para determinar o volume desse sólido utiliza o método da casca.
Vocês lembram o que diz esse método?
Basicamente, ele fala que se rotacionarmos uma região abaixo da curva em torno do eixo , o volume do sólido obtido vale:
Massa! Vamos então montar a nossa integral pra calcular o volume do sólido de revolução.
Passo 2
Como comentamos no passo , nossa região está abaixo da curva:
No intervalo:
Assim, como pelo método da casca:
Temos:
Puts, e como calculamos essa integral??
Podemos usar a ideia da mudança de variáveis, fazendo:
Além disso, quando :
E, quando :
Substituindo na integral, e tirando as constantes para fora do integrando, temos:
Usando que:
Temos:
Portanto:
E é isso galera, espero que vocês tenham acompanhado até aqui. Um abraço e até a próxima 😊