Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cascas Cilíndricas

Ver Teoria
Exercício 361234567891011121314151617181920212223242526272829303132333435373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UnB – Cálculo 1 – Lista de Exercícios 14 – Questão 5c

Seja a ≥ 0 , f : a , b → [ 0 , + ∞ ) uma função contínua e R   a região compreendida entre o gráfico de f e o eixo O x . Quando giramos a região R em torno do eixo O y , obtemos um sólido de revolução cujo volume é dado por V = ∫ a b 2 π x   f ( x ) d x . Calcule esse volume no caso as funções indicadas abaixo

c )   f x = arctan ⁡ x ,   p a r a   x ∈ [ 0,1 ]

Passo 1

Fala galera, tudo bem? Essa questão parece complicada, mas vou te ajudar!

O problema nos deu essa função aqui

f x = arctan ⁡ x

Entre o intervalo [ 0,1 ] e disse que o volume do sólido de revolução em torno do eixo horizontal é

V = ∫ a b 2 π x   f x d x

Em que a , b são os limites do intervalo!

Anota aí!

E pediu para calcularmos esse volume! Então nossa missão é substituir a função na integral para V , identificar qual método usar e #partiu integração!

e é isso! Mas relaxa que vou fazer passo a passo com você!

Vamos começar?

Passo 2

Nossa função é

f x = arctan ⁡ x

Os limites são 0 , 1 , então temos

V = ∫ 0 1 2 π x [ arctan ⁡ x ] d x = 2 π ∫ 0 1 x arctan ⁡ x d x

Agora nossa missão é integrar essa coisa! Vamos calcular a integral indefinida, para depois aplicar nos limites

V = ∫ x arctan ⁡ x   d x

Como vimos nessa lista, integrais que tem como integrando o produto de uma função algébrica por uma logarítmica a gente resolve pelo método: integração por partes

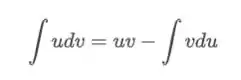
u e quem é d v ? E aqui vai um truque super útil: seguir a tabelinha do LIATE

No nosso caso u = arctan ⁡ x e d v = x d x , assim

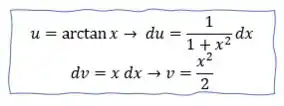
E aplicando por partes na nossa integral temos:

∫ x arctan ⁡ x d x = x 2 2 arctan ⁡ x - ∫ x 2 2 . 1 1 + x 2 d x = x 2 2 arctan ⁡ x - 1 2 ∫ x 2 1 + x 2   d x

Beleza?

Passo 3

Chegamos a esse resultado aqui

∫ x arctan ⁡ x d x = x 2 2 arctan ⁡ x - 1 2 ∫ x 2 1 + x 2   d x

Agora nossa integral recaiu em outra integral! Aparentemente ela é ingênua! Mas saca só: não podemos usar substituição simples chamando u = 1 + x 2 , pois assim o d u = 2 x   d x e vai ficar sobrando um x na nossa integral!

E agora? Como resolver?

ALERTA TRUQUE SUJO

Vamos somar 1 e subtrair 1 no numerador

x 2 + 1 - 1 1 + x 2

Assim podemos separar essa fração algébrica em duas:

x 2 + 1 1 + x 2 - 1 1 + x 2 = 1 - 1 1 + x 2

E agora? Agora ficamos com duas integrais: sendo que uma é a integral de 1 e a outra é a integral de 1 1 + x 2 que é o arco tangente!

Retomando nossa integral

∫ x arctan ⁡ x d x = x 2 2 arctan ⁡ x - 1 2 ∫ x 2 1 + x 2   d x

E aplicando o truque sujo na integral da direita temos

∫ x arctan ⁡ x d x = x 2 2 arctan ⁡ x - 1 2 ∫ x 2 + 1 - 1 1 + x 2   d x = x 2 2 arctan ⁡ x - 1 2 ∫ x 2 + 1 1 + x 2 - 1 1 + x 2 d x

Separando em duas integrais mais simples:

∫ x arctan ⁡ x d x = x 2 2 arctan ⁡ x - 1 2 ∫ 1 d x - ∫ 1 1 + x 2 d x =

E aí é só integrar!

= x 2 2 arctan ⁡ x - x 2 + 1 2 arctan ⁡ x

Tudo bem até aqui?

Bora aplicar os limites de integração!

Passo 4

Agora vamos aplicar os limites de integração na integral indefinida que acabamos de calcular!

Tínhamos o seguinte

V = 2 π ∫ 0 1 x arctan ⁡ x d x

Mas a integral indefinida ∫ x arctan ⁡ x d x vale

∫ x arctan ⁡ x d x = x 2 2 arctan ⁡ x - x 2 + 1 2 arctan ⁡ x  

Beleza?

Então o volume do nosso sólido de revolução é

V = 2 π x 2 2 arctan ⁡ x - x 2 + 1 2 arctan ⁡ x 0 1 =

2 π 1 2 2 arctan ⁡ 1 - 1 2 + 1 2 arctan ⁡ 1 - 2 π 0 2 2 arctan ⁡ 0 - 0 2 + 1 2 arctan ⁡ 0

Fazendo as contas teremos o volume desse sólido:

V = 2 π π - 2 4 = π 2 - 2 π 4

E é isso! Espero ter ajudado!

Resposta

π 2 - 2 π 4

Exercícios de Livros Relacionados

Nos Exercícios 23-26, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões delimitadas pelas curvas dadas em torno das retas dadas.26 - y = x 4ey = 4 - 3 x 2 B
Para algumas regiões, os dois métodos funcionam bem para sólidos obtidos com a rotação da região em torno dos eixos das coordenadas, mas isso nem sempre ocorre. Por exemplo, quando uma região gira em