A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método.
b. em torno do eixo y.
Passo 1
Fala turminha beleza? Bora lá! A maior dificuldade dessa questão tá na gente conseguir imaginar como ficaria o gráfico dessa questão. Temos isso aqui:
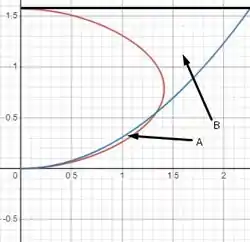
Passo 2
Dividindo a o gráfico em duas regiões de rotação, vai facilitar nossa vida. A gente faz eles separados e depois soma. Primeiro calculando a região A:
Para os limites de integração, precisamos achar esse ponto aqui:
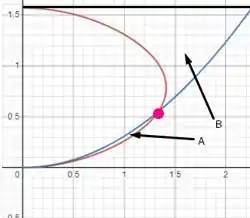
É ele quem vai nos dizer até aonde vamos integrar o nosso volume A. Para achar ele precisamos igualar as equações e saber aonde se tocam. Então a gente faz assim:
Passo 3
Beleza, agora temos dois caminhos. Primeiro é resolver essa equação da maneira tradicional, mas ela vai ficar muuuuito grande extensa. Pelo intervalo trigonométrico e pelo valor próximo do gráfico, podemos inferir que o intervalo vai de 0 até . Portanto,
Resolvendo essa integral:
Passo 4
Agora calculando o volume de B, vamos primeiro atrás dos intervalos de integração. Como ele começa aonde o nossa região A acaba, e ele termina categoricamente em , temos o seguinte:
Como ja temos o valor de cada integral pré montado no passo passado, ja podemos calcular direto o valor. Temos então que:
E agora pra finalizar,
Somando os dois volumes: