Cálculo de Volumes através de Integrais
Seja . Considere a região ilimitada , entre o eixo , o gráfico de , a reta e a reta . Calcule, se possível, o volume obtido pela rotação de ao redor da reta .
Passo 1
Cara, a reta é basicamente um eixo paralelo ao eixo só que passando no ponto , e essa é como o gráfico da hipérbole deslocado uma unidade para frente. Olha como ficaria o nosso esboço:
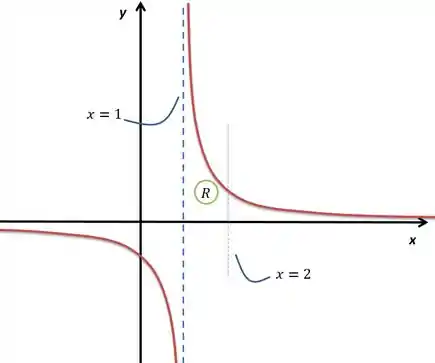
Como pedido, a região ilimitada, entre e . Rotação em torno de um eixo paralelo a costuma ser mais simples quando fazemos por casca cilíndrica:
Passo 2
Nesse caso, o raio da casca será menos o eixo, ou seja . Já o é a própria função. Com isso,
Resposta
Exercícios de Livros Relacionados
Nos Exercícios 23-26, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões delimitadas pelas curvas dadas em torno das retas dadas.26 - y = x 4ey = 4 - 3 x 2 B
Para algumas regiões, os dois métodos funcionam bem para sólidos obtidos com a rotação da região em torno dos eixos das coordenadas, mas isso nem sempre ocorre. Por exemplo, quando uma região gira em