Considere as funções e e a região plana descrita abaixo:
Seja o sólido de revolução obtido pela rotação de em torno do eixo
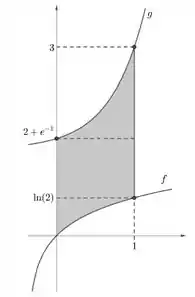
- Esboce a região
- Determine e (as expressões das funções inversas de e , respectivamente)
- Utilizando o método que preferir, escreva o volume de como uma integral ou soma de integrais. Obs.: Neste item não é necessário calcular o volume
Passo 1
Opa, vamos lá. Antes de mais nada, vamos precisar fazer um bom esboço. Afinal, ele que vai nos ajudar a montar a equação do volume depois. Vamos ver primeiro isso aqui:
Pra função que delimita por baixo, temos:
Pra esboçar essa curva é interessante a gente lembrar que pra funções logarítmas:
Mas como também ta valendo pra , temos que considerar essa curva só a partir do eixo . E quando ela toca esse eixo? Vamos ver?
Show de bola, agora pra curva que delimita por cima:
É interessante lembrarmos que das propriedades das exponenciais:
Mas como também, só vamos nos preocupar com a parte dessa curva que tá a direita do eixo . Opa, vai ser interessante então eu também anotar em que ponto que a curva toca esse eixo:
E pra fechar basta só a gente olhar para a condição . Para a curva de cima e de baixo, respectivamente, teremos o seguinte valor de para esse valor de :
E olha só! Temos o suficiente pra esboçar agora! Bora lá então:
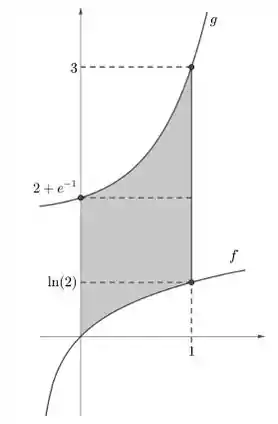
Passo 2
Bora pras funções inversas então. As normais são essas:
Pra achar a inversa, basta a gente isolar nos dois casos e depois trocar de lugar o com . Pro primeiro caso, temos:
Trocando de lugar:
Bora terminar essa letra da questão achando a inversa de :
Trocando de lugar:
Passo 3
Só falta mais uma coisita pra gente partir pro abraço! A fórmula do calcul do volume. Bem, como ele quer rotação em torno do eixo , podemos usar o Método das Cascas logo de cara. Se entendermos a região como uma região maior verde subtraída de uma menor cinza...
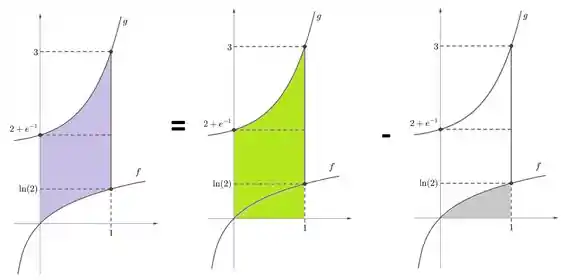
Para o volume do sólido de rotação, poderemos considerar a mesma coisa:
A vantagem que a gente tem é que cada cor corresponde a uma função somente, então a montagem da fórmula do volume é direta ao ponto, só usar a curva correspondente a cada cor e os limites de integração dados do enunciado: