Seja a região plana definida por:
Considere o sólido de revolução obtido através da rotação da região em torno do eixo .
(a) Esboce a região
(b) Usando o método que preferir, escreva o volume de S como uma integral ou como uma soma de integrais.
(c) Calcule o volume de S.
Passo 1
(a)Esboçar as limitações em
Vamos com calma que esboço de gráfico ou, no caso, regiões as vezes enrola a cabeça. Começando com o que é mais tranquilo, pelo enunciado, o menor valor possível de é e o maior valor possível é . Então nossa região está entre essas duas retas verticais:

Passo 2
Esboçar as limitações em
Show, vamos ver agora as limitações em . Pelo enunciado:
Agora, saca só: quando está no seu ponto mínimo, que é , o vai estar entre:
Vamos então marcar esses pontos:
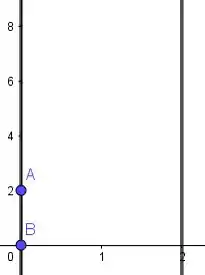
E quando quando está no seu ponto máximo, que é , o vai estar entre:
Marcando esses pontos:
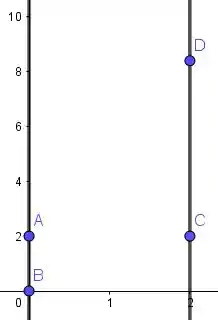
Tudo o que falta agora é ligar os pontos até e até . Só que como é limitado por duas funções, o caminho que esses pontos vão fazer até se ligarem é a própria curva dessas funções. Beleeeza, vamos então traçar.
Ligamos até pela função que limita por cima, que é a função exponencial . Sendo assim:
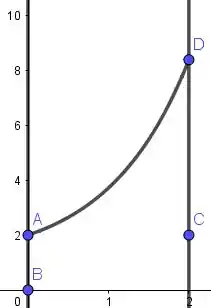
E pra gente fechar e partir pro abraço, ligamos até pela função que limita por cima, que é a reta . Sendo assim:
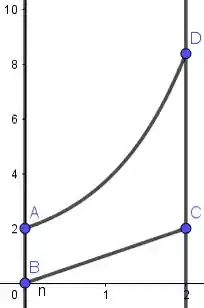
Nossa região então vai ser o que está dentro, logo:
Passo 3
(a) Escolher um método e escrever a integral
Pra gente conseguir escrever a integral, vamos pensar nossa região de uma forma diferente. Nossa região que era:
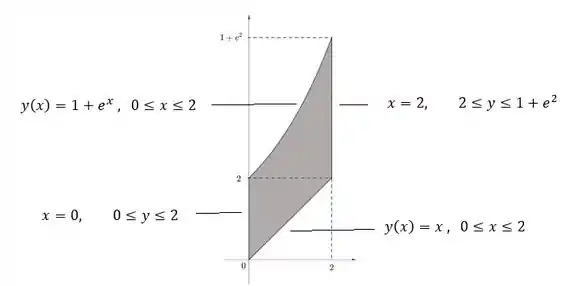
Pode ser “deitada” se invertermos as funções e escrevêssemos elas como funções . Partiu então?
Graficamente:
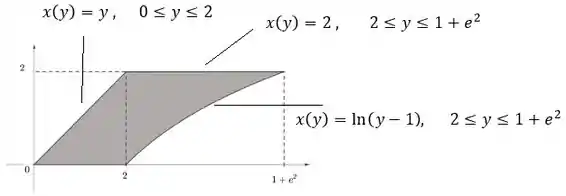
O volume de uma região qualquer, pelo método dos discos, vai ser então:
E agora basta a gente entender como usar essa fórmula. Dá uma olhada aqui:
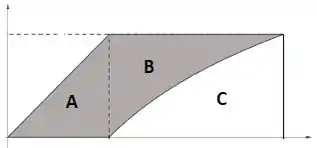
A região , quando revolucionada, gera um cone, a região , um cilindro e a região , meio que um “copo”. Como a região é igual à , temos que diminuir do volume do cilidro o volume do copo. Ou seja, nosso volume vai ficar:
Passo 4
(b) Resolvendo a primeira integral
Agora é só trabalho braçal pra resolver a integral mesmo. Vamos aos poucos pra não nos confundirmos. A primeira integral vai ser:
E resolvendo a malandra, vamos ter:
Passo 5
(b) Resolvendo a segunda integral
A segunda integral vai ser:
Essa ai também tiramos de letra, só partir pra resolução:
Passo 6
(b) Resolvendo a terceira integral
Essa vai ser a integral mais complicadinha de resolver. A terceira vai ser:
Vamos primeiro fazer uma substituição simples pra tirar o dai. Vamos fazer:
Se fizermos:
Vamos poder integrar por partes e ficar com:
E aplicando os limites de integração:
Infelizmente vamos ter que integrar por partes de novo porque ainda sobrou um logarítimo dentro da integral. Se fizermos:
Ficamos com:
Aeee, sem integrais restantes! Agora vamos juntar os resultados todos. Mas antes, vamos aplicar os limites de integração de novo:
Agora vamos unir todos os resultados. O que a gente achou foi:
Então se juntarmos tudo no liquidificador e apertar o Start:
Passo 7
(b) Juntando o resultado das 3 integrais
Ufa, finalmente. Pra terminarmos e acharmos o volume a gente só precisa unir o resultado das 3 integrais. Vamos lá então e depois é só partir pro abraço:
Resposta
(a) 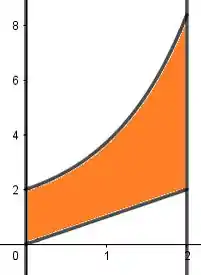
(b)
(c)